MA 323A Combinatorial Geometry!
Notes on Buckyballs -- Part 2
The first Part of the Buckyball notes describes a class of Buckyballs,
which I'm calling the pentagons pointing-in, or PPI family,
where the "tiles" that correspond to the faces of the icosahedron are
made by triangulating each face of the icosahedron and taking the dual.
But we noticed that the classic spherical Buckyball known as the soccer
ball (or truncated icosahedron) does NOT fit into this family!
Thus there are other Buckyballs out there. What are they? How can
we find them?
First let's look at what the dual of the soccer ball really looks like:
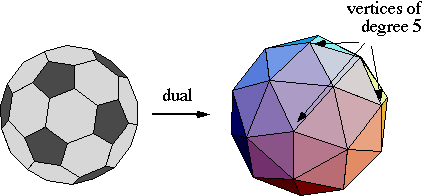 Clearly this dual is not just an icosahedron with triangulated faces.
The arrangement of triangles in between three near-by vertices of degree 5
is more complicated. This can be examined more closely by looking
at what a "tile" of neighboring pentagons looks like on the soccer ball:
Clearly this dual is not just an icosahedron with triangulated faces.
The arrangement of triangles in between three near-by vertices of degree 5
is more complicated. This can be examined more closely by looking
at what a "tile" of neighboring pentagons looks like on the soccer ball:
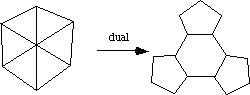 Hmmm ... This tile has the pentagons "pointing-out", whereas in the
tiles for the other Buckyballs we've seen the pentagons are pointing-in.
This suggests a different class of Buckyballs, which I like to call
the pentagons pointing-out (PPO) family. Indeed, arranging
more hexagons in between the pentagons gives you bigger tiles, and thus bigger
PPO spherical Buckyballs.
Hmmm ... This tile has the pentagons "pointing-out", whereas in the
tiles for the other Buckyballs we've seen the pentagons are pointing-in.
This suggests a different class of Buckyballs, which I like to call
the pentagons pointing-out (PPO) family. Indeed, arranging
more hexagons in between the pentagons gives you bigger tiles, and thus bigger
PPO spherical Buckyballs.
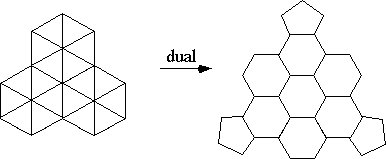 The above tile is the next largest one in the PPO family, after the
soccer ball. The soccer ball requires 90 PHiZZ units to create. The
above tile takes 360 units to make into a spherical Buckyball.
The above tile is the next largest one in the PPO family, after the
soccer ball. The soccer ball requires 90 PHiZZ units to create. The
above tile takes 360 units to make into a spherical Buckyball.
Exercise: In the PPI family, let n=1 be the dodecahedron (which has 30
edges, thus needing 30 units to make) and n=2 be the next one in this family
(which we saw in Part 1, having 120 edges). Find a formula in terms of
n for the number of edges in the nth member of the PPI family.
Then let n=1 be the soccer ball in the PPO family, and n=2 be the next
biggest one, whose tile is shown about. (360 edges.) Find a formula
in terms of n for the number of edges in the nth member of the PPO
family.
But is this it?? Do all spherical Buckyballs fit into either the PPI family
or the PPO family? The answer is NO! Having the pentagons "pointing in" and
"pointing out" are only two possibilities. We can actually rotate each
pentagon a little bit and create other families of spherical Buckyballs!
But is there any way to classify these? You betcha!
More to come...
Return to Combinatorial Geometry Page
|


