MA 323A Combinatorial Geometry!

Notes on Graph Colorings
As we examine different types of polyhedra and different types of combinatorial structures, the subject of colorings will arise and entertain us all! By a coloring of a graph we mean an assignment of colors (which we sometimes denote by numbers) to the various parts of the graph, like the vertices, edges, or faces. It is usually implied that such colorings are proper colorings, meaning that any pieces that touch must receive different colors. To be more precise,

Definition: Let G be a graph. Then
  • a vertex coloring is an assignment of colors to the vertices of G,
  • an edge coloring is an assignment of colors to the edges of G, and
  • a face coloring is an assignment of colors to the faces of G, providing that G is a planar graph.
Now, if we allow ourselves to use enough colors, then coming up with a proper coloring of a graph can be very easy. The hard part is finding the fewest number of colors we can use to color the vertices, edges, or faces of a graph. In this vein we define,

Definition: A graph is k-vertex colorable if we can properly color the vertices of the graph using only k different colors.
Similarly, we define k-edge colorable and k-face colorable.

Definition: The chromatic number of a graph G is the fewest number of colors we can use to properly color the vertices of G. This number is denoted X(G). (Actually, that's not supposed to be an X, it's supposed to be the Greek letter chi, but I don't know how to get HTML to produce that character. Sorry!) More formally, we can define
X(G) = min { k : G is k-vertex colorable }
We also sometimes talk about the edge-chromatic number, denoted by X'(G).

Example: What is the chromatic number of the octahedron, O?
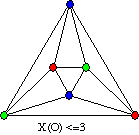
The above picture shows a proper 3-vertex coloring of the octahedron, and therefore we know that X(O)< = 3. Also, there's no way that we could vertex color the octahedron with only 2 colors, because the triangles in this graph require 3 colors at the very least! Thus we may conclude that X(O)=3.

What follows is a listing of Theorems about graph colorings. Some will be proven in class.

The Four Color Theorem: Every planar graph is 4-vertex colorable.

The Four Color Theorem (FCT) has a great history - it remained an open conjecture for a hundred years until Appel, Hacken, and Koch proved it was true by reducing it to almost 2000 subcases and writing a computer program to check all these cases. Thus, while this Theorem is considered to be proven, people still search for a shorter proof. It's also just, plain amazing that such a simple-to-state Theorem would be so incredibly difficult to prove.

The FCT can be re-stated in many different ways. The following versions of the FCT pertain to some of the colorings we've already explored in class:

Theorem: The following three statements are equivalent:
  1. Every planar graph is 4-vertex colorable.
  2. Every planar graph is 4-face colorable.
  3. Every 2-edge connected cubic planar graph is 3-edge colorable.
Note: cubic means that every vertex has degree 3. 2-edge connected means that in order to disconnect the graph you must remove at least 2 edges.

Also note: The first two are equivalent because we can just take the dual of the planar graph and turn vertex colorings into face colorings, and vice-versa. The third one is harder to show -- we proved it in class.

In other words, the 3-edge colorings that we've been making of the dodecahedron and Buckyballs and various things using Sonobe units are equivalent, in a sense, to 4-vertex colorings of general planar graphs. Weird! Also, this allows us to appreciate how difficult 3-edge coloring cubic planar graphs can be, since 4 coloring planar graphs can be very difficult.

Not surprisingly, it is much easier to characterize when a graph is 2-vertex colorable. The following Theorem does just this.

The Two Color Theorem: A graph is 2-vertex colorable if and only if the graph has no odd cycles.

Another way to state that is this: A graph is 2-vertex colorable if and only if it is bipartite. This is very easy to prove, and we'll probably do it in class.

Of course, there is also a Three Color Theorem, but it's a little bit harder to state. To see where it comes from, look at a class of graphs called wheels. A wheel is a graph that consists of a cycle and one vertex in the "middle" which is connected to all the vertices on the cycle. (See the picture below.) An odd wheel is a wheel whose outer cycle is of odd length, and an even wheel has an even cycle for the "rim."
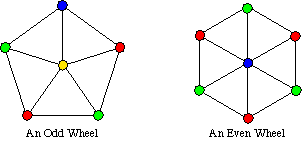
Clearly even wheels have chromatic number 3 and odd wheels have chromatic number 4. So it seems like odd wheel configurations definitely need to be avoided if we want a graph to be 3-vertex colorable, right? Well, it turns out that, for planar graphs at least, avoiding odd wheels is enough to guarantee 3 colorability!

The Three Color Theorem: A planar graph that has all triangle faces is 3-vertex colorable if and only if every vertex has even degree.

One direction of the proof of this Theorem is easy. (Which one?) The other direction can be done in a really cool way by induction on the number of vertices. Oooo!

Here's another good one, which is also REALLY hard to prove!

Grötzsch's Theorem: Every planar graph with no 3-cycles is 3-vertex colorable. (That is, triangle-free planar graphs are 3-vertex colorable!)

There are many, many more coloring Theorems. A whole course could be taught on graph colorings! But for now realize what we've learned about some of the graphs we've been examining: Every cubic planar graph (that is 2-edge connected) is 3-edge colorable. That is, we know that all those Buckyballs that we've been making from PHiZZ units can be properly 3-edge colored. The question is HOW? Just because we know we can do it doesn't mean that it's easy!

Exercise: What do these coloring Theorems say about how many colors we'll need if we use Sonobe units to make "versions" of polyhedra? Will 3 colors always be enough?

Return to Combinatorial Geometry Page