MA 323A Combinatorial Geometry!

Notes on Spherical and Convex Polyhedral Geometry
Note that we explored spherical geometry in class by drawing "straight lines" on oranges. We saw that on a sphere straight lines are actually great circles. By messing around with our oranges and our magic markers, we managed to discover the following:

Theorem: On a sphere of radius r, the area of a wedge made by two intersecting lines with internal angles is
2r2

The proof we gave of the above Theorem wasn't very rigorous. It might make a neat project for someone to find a down-and-dirty proof of this, either on their own or in a book somewhere.

Theorem: The area of a spherical triangle with internal angles 1, 2, and 3 on a sphere of radius r is
(1 + 2 + 3 - ) r2

We did prove this one rigorously! And it was fun too, wasn't it?

In general, we can get a similar formula for the area of any spherical polygon, whish is called the spherical excess formula:

Spherical Excess Formula: The area of an n-sided spherical polygon with internal angles 1, 2, 3, ... n on a sphere of radius r is
(1 + 2 + 3 + ... + n - (n-2) ) r2
How would you prove this? Is it hard? Easy?

For more fun things to think about spherical geometry, see the book Experiencing Geometry on the Plane and Sphere by David Henderson, Prentice Hall, 1996.

The pointyness of a corner

We then turned our attention to exploring the differences between plane angles (angles drawn in the x-y plane) and solid angles (3D angles, like the corner of a cube or a corner of any polyhedron). Plane angles are measured in either degrees of radians. But how do we measure solid angles?

One way is to measure the solid angle's deficiency. This is the "gap" left over if we flatten the solid angle out after cutting along one of its edges. More technically, if a solid angle A is made up of plane angles A1, A2, ..., An, then
The deficiency of A = 2 - (A1 + A2 + ... + An).
(Note: That's supposed to be "2 times pi", not "2 raised-to-the-pi". You gotta love these wacky gif images!!)

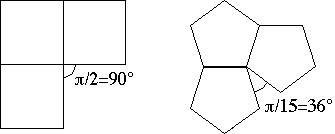
The deficiency of a cube is 90 degrees at a corner, and
the deficiency of a dodecahedron is 36 degrees at a corner.


Another way to measure solid angles, called the solid angle measure, is analagous to the way plane angles are measured in radians. For radians, we take the given angle we wish to measure and center at the angle a circle of radius one. The length of the arc that the angle cuts out of the circle is called the radian measure of the angle.
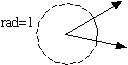
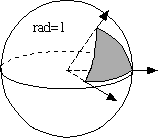
So why can't we do the same thing with solid angles? Indeed, we can! Take your favorite solid angle and center a sphere of radius one at the corner. The solid angle will "cut out" a spherical polygon from the sphere, and the area of this spherical polygon is called the measure of this solid angle. (Instead of radians, the units used for solid angles are called steradians.)

The area of the gray spherical triangle is the measure of the solid angle.

Now perhaps you can see the connection between spherical geometry and polyhedra! If we want to measure a solid angle we'll need to use the spherical excess formula. But what will the interior angles of the spherical polygon be? Because the solid angle is positioned at the center of the sphere, the edges of the solid angle will intersect the sphere at right angles. Thus the interior angles of the spherical polygon will be the same as the angles between the planes of the solid angle! That's a mouthful. We need a definition.

Definition: A 3D solid angle contains two types of ordinary, plane angles:
  1. The plane angles which are the angles, based at the corner, of each plane face of the solid angle, and
  2. The dihedral angles which are the angles between two adjacent planes of the solid angle.

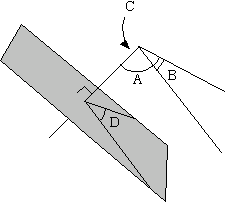
A, B, and C are plane angles, while D is a dihedral angle.

Dihedral angles can be tricky to visualize. You measure the dihedral angle between two planes, P1 and P2, of a solid angle by inserting a plane that is perpendicular to the edge between P1 and P2, and then measuring the 2D angle that's cut out on this plane between P1 and P2. But the important connection to make is:
the dihedral angles of a solid angle are equal to
the internal angles of the spherical polygon made when we measure the solid angle.



Another concept that we can borrow from 2D plane geometry is that of supplementary angles. In 2D land, you can find the supplementary angle of an ordinary angle by drawing perpendicular lines from the sides of the angle, seeing where they intersect, and measuring that angle.

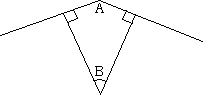
In the above picture, angle B is the supplementary angle of angle A. Notice that an angle and its supplementary angle are complimentary. That is, in the above picture we have A + B = , or 180 degrees.

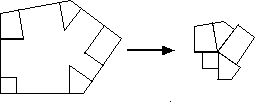
Exercise: Prove that for any polygon, the sum of the supplementary angles is always 2, or 360 degrees. The below picture might help.


So can we find supplementary angles to solid angles in 3D land? You betcha! We call them supplementary solid angles.

Take a 3D solid angle. Instead of making perpendicular lines from each side, we'll now have to make perpendicular planes from each side of the solid angle. These will meet at a point, and this point will form the supplementary solid angle of the original solid angle. This is gosh-darned hard to visualize! Hopefully the below picture will help. (The weird arrow-head-like marks are supposed to be "right angle" symbols drawn in 3D to illustrate which planes are perpendicular.)

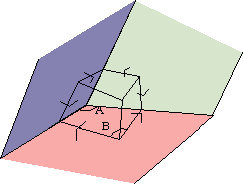
Constructing a supplementary solid angle. (You're looking into the solid angle here.)

There are lots of things to say about supplementary solid angles. The proofs of the following facts are left for you! (Or will be done in class...)
  • in the above picture, angles A + B = , or 180 degrees.
  • The sum of the measures of the supplementary angles at every corner of a polyhedron always equals 4, or 720 degrees.
Wow! That last one is a doozy! But it should make sense, right? Think about how the 2D case works.


Now it's time to put all sorts of pieces together and prove a BIG THEOREM! Here are the pieces:
  • The sum of all the supp. solid angles of the corners of a polyhedron = 4.
  • The Spherical Excess Formula.
  • The fact that the internal angles of spherical polygons that we get when measuring solid angles are just the dihedral angles of the solid angle. (Salad angle? ; )
  • Angle B in the above picture is a dihedral angle of the supplementary solid angle shown, and we know B = -A.
  • Angle A in the above picture is just one of the plane angles of the original polyhedron!
  • Plane angles are used to measure the deficiency of a solid angle.

In the mid 1600s, the philosopher and mathematican Rene Descartes put all these pieces together and came up with a wild Theorem:

Descartes' Theorem: The sum of the deficiencies of the solid angles in a polyhedron is always equal to 4.

Can you put the pieces together in the right order to prove this?

Descartes' Theorem is really fun. You can use it to give a different proof that every Buckyball must have exactly 12 pentagon faces. (We'll do this in class.) You can even use it to prove Euler's Formula for polyhedra! Hot dang!

Interesting Project Idea: There are a number of web pages that also have tutorials on spherical, and convex polyhedral geometry. For example, look at http://www.inetarena.com/~pdx4d/ocn/limits0.html titled Descartes' Deficit. What is this web page trying to say? Is it making any sense? What about other web pages that you can find? Remember: not everything you read on the web is true. (Including, possibly, here!)
Return to Combinatorial Geometry Page