MA 323A Combinatorial Geometry!
Notes on Flat Folding
how can we tell if this is a crease pattern for some origami model?
This is a VERY HARD problem! In general, it is completely unsolved. In fact, it's very hard to know how to attempt an answer because one needs to define words like "origami" mathematically. That, alone, can be problematic.
A good place to start is to restrict ourselves to flat folds, that is, origami models that are flat - can be pressed in a book without adding new creases. Most of the origami models that are found in origami books fall into this category. In fact, if we could answer the above question for any potential flat fold, it would go a long way towards helping us learn how to design origami models, like animals and insects and stuff!
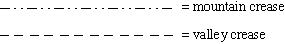
The above terminology is essential, since the words mountain and valley crease describe the two types of creases we might find in a flat origami model crease pattern. Using these two types of dashed lines to distinguish them is the standard notation used in origami books.
Above is shown the crease pattern of the classic "flapping bird" model, as well as what it looks like when folded flat. Staring at crease patterns like this can be confusing. It's hard to tell what all the crease lines are doing when everything folds flat! Therefore we will first examine flat vertex folds, which are crease patterns that have only one vertex. Below are some examples:
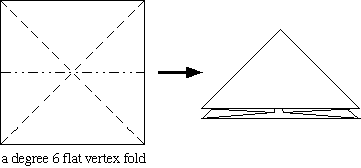
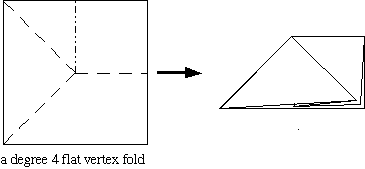
Exercise: Get some pieces of paper and create your own flat vertex folds. How many creases can you make meet at a vertex and have them fold flat? Can you ever get an odd number of creases? What about the number of mountain creases you see and the number of valley creases? Do you see a pattern?
Don't read ahead until you play with this exercise! It's fun to discover these things for yourself!
After a fair amount of experimentaion, you might notice that the number of mountains and the number of valleys always seems to differ by 2. This always happens in flat vertex folds. This result is called Maekawa's Theorem, after the Japanese physicist Jun Maekawa, who is also the creator of many complex origami models, like the Winged Demon that's shown on the main Combinatorial Geometry page. This was first called "Maekawa's Theorem" in the book Origami for the Connoisseur by K. Kasahara and T. Takahama (Japan Publications, 1987), but this book had been published several years before in Japanese under the name Top Origami. However, the French mathematician Jacques Justin also discovered this result and published it in British Origami (the magazine of the British Origami Society), June, 1986, p. 30. Neither of these references contain a proof of the Theorem, and the one given here was developed by Jan Siwanowicz, then a high school student, at the 1993 Hampshire College Summer Studies in Mathematics.
Maekawa's Theorem: The difference between the number of mountain creases and the number of valley creases in a flat vertex fold is always 2.
Proof: Let n = the number of creases adjacent to v, a flat vertex fold. Let M = the number of mountain creases and V = the number of valley creases adjacent to v. Then n=M+V.
Let's fold the paper flat. Then the vertex in the crease pattern will become a point in the folded figure. If we cut, or truncate this point off the folded figure, then a polygonal cross-section will be revealed. (See below.)
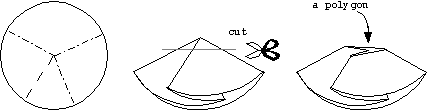
In fact, this polygonal cross section is a flat polygon, whose interior angles are either 0 or 360 degrees. Also, if we look at the folded figure from above, as shown in the picture, then the mountain creases in the crease pattern will correspond to 0 degree angles in the flat polygon, and valley creases will correspond to the 360 degree angles.
Hmmm ... but n is the number of creases, which equals the number of corners of our flat polygon, which equals the number of sides of our flat polygon. Ah ha! And recall that the sum of the interior angles of any polygon with n sides is equal to (n-2)180 degrees! Using the fact that each mountain crease adds 0 degrees and each valley adds 360 degrees, and n=M+V, we get
Of course, if we had looked at the folded figure from below then we would have gotten M-V=-2. This completes the proof! Q.E.D.
Corollary: The degree of the vertex in a flat vertex fold must always be even.
Proof: Let n = the degree of the vertex. As the vertex will satisfy Maekawa's Theorem we have n = M+V = M - V + 2V = 2 ( ± 1 + V) which is an even number. Q.E.D.
Another cool Corollary which can be proven from the above Corollary is the following, which I believe was first discovered by Meguro of Japan:
Corollary: (Meguro) The faces of the crease pattern of any flat origami fold are always 2-face colorable.
For a hint at the proof, consider the dual of the crease pattern, and try to apply the Two Color Theorem!
Our second Theorem is also commonly named after a Japanese paperfolder, Kawasaki, and was first referenced as such in Origami for the Connoisseur. However, Jacques Justin, in the same British Origami article mentioned above, also discovered it. (Neither reference, again, contains a proof, although I'm sure that both Kawasaki and Justin knew proofs. The one below was developed by me and published in "On the Mathematics of Flat Origamis", Congressus Numerantium, Vol. 100 (1994), pp. 215-224.)
Kawasaki's Theorem: The sum of every other angle about the vertex in a flat vertex fold is always 180 degree.
Proof: Let
i denote the angles around the vertex, where
i = 1, 2, 3, ..., 2n. We fold the paper into a folded figure, and imagine we are
an ant that is standing on the "first" crease, next to angle
1. The ant, being an ant, can't stand still, and
thus walks
on the folded figure around the vertex. (Thus, if we were to track the position
of the ant on the (unfolded) crease pattern, the ant's path would be a circle
going around the vertex.) The situation, in the degree 4 case, is illustrated
below.
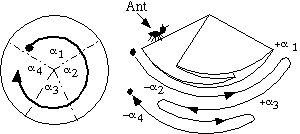
As the ant walks on the paper, it will walk along the angles, starting with
1. When it reaches the next crease
line, it will switch directions and walk along angle
2. Continuing in this way, we can
say that the ant is walking in the "positive direction" on
every angle with an odd index, and in the "negative direction" on
every angle with an even index. Further, when the ant completes its
journey, the ant will be back at the beginning, meaning that the
resulting sum of the angles must be zero. That is,
1 -
2 +
3 - ... -
2n = 0.
Ah, but the sum of these angles must be 360 degrees, right? Adding the above to the equation
1 +
2 +
3 + ... +
2n = 360
gives us,
1 +
23 +
25 + ... +
22n-1 = 360.
Dividing by 2 gives us that the sum of every other angle, starting with
1 equals 180 degrees. The corresponding
formula, beginning with
2 can then be easily obtained as well.
Q.E.D.
Exercise: Prove that the converse of Kawasaki's Theorem is also true! (Hint: you may have to try some origami mutilation, like cutting, to prove that the paper folds flat.)
That last exercise is a big one. It proves that the "180 degree condition" is necessary and sufficient for a crease pattern with only one vertex to fold flat. In other words, this describes completely how crease patterns locally fold flat, at each vertex.
But does the 180 degree condition describe how crease patterns gloabally fold flat as well? The answer is NO! Indeed, there are crease patterns with more than one vertex that satisfy the 180 degree condition at each vertex, but which do not fold flat. Below is shown the smallest known example of such an "impossible fold." (This appeared in my Congressus Numerantium article, cited above.)
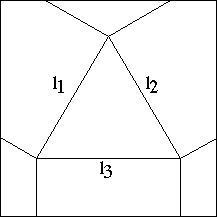
Exercise: Why can't the above crease pattern fold flat?
Return to Combinatorial Geometry Page