MA 323A Combinatorial Geometry!
Notes on Planar Graph Theory
Definition: A graph G is any network of points and lines. We usually call the points vertices and the lines edges. Since every graph is determined by it's set of vertices and edges, we usually denote a graph by G=< V,E> .
A graph is called a planar graph if it is drawn in such a way that the edges never cross, except at where they meet at vertices.
There is a direct connection between polyhedra and planar graphs, namely that we can take any polyhedron and "project" it down onto a flat piece of paper, turning it into a graph. This is sometimes nice to do because graphs are easier to draw than 3D polyhedra, and the planar graph contains all the network structure information of the polyhedron, like how many vertices, edges, and faces it has. Below is shown how we can turn the cube into a planar graph.
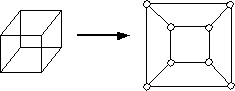
In class we drew the planar graphs of other polyhedra, like
Definition: If G is the graph of a polyhedron, let G* denote the graph of the planar dual of G. We construct G* in the following way:
- for every face of G we make a vertex of G*, and
- two vertices in G* will form an edge if and only if the corresponding faces in G are next to one another (that is, they share an edge).
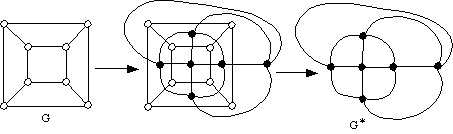
But look! If we re-arrange the vertices in the dual G* we get the following:
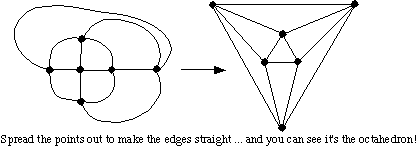
Thus we see that the dual of the cube is the octahedron! Wow! It also makes sense that if we took the dual of the octahedron then we'd get the cube back, right?
Euler's Formula
The following are some things that we learned on the Thursday, Jan. 27th class, or things that we'll be learning soon!Euler's Formula: If G is a planar graph with V vertices and E edges and F faces, then we have the following formula:
We'll be proving Euler's Formula in class, and the proof will be by induction! So get ready for it.
Now, I mentioned in class that we can use Euler's Formula to prove that there are exactly 5 Platonic solids, and I ask you to do this yourself on an upcoming problem set. Here are some notes that help you get started:
Definition: If v is a vertex in a graph, then the degree of v is the number of edges coming out of v. We denote this by deg(v).
Similarly, the degree of a face f in a planar graph is the number of edges going around the face. (Thus a triangle face has degree 3, a hexagon face has degree 6, etc.) We denote this by deg(f).
Here's a classic graph theory Theorem:
Theorem: Let G be any graph and let E be the number of edges in G. Then if v1, v2, v3, ... vn denote the vertices in G, we have
Proof: Go to every vertex in G and add up the number of edges coming out of that vertex. This is just suming up the degrees of the vertices, so we'll get the left-hand side of the above formula. On the other hand, this will be adding up the total number of edges in the graph, EXCEPT that we'll actually be counting each edge twice, right? This is because each edge is adjacent to two vertices. So if an edge e is connecting vertices vi and vj, we'll count e once at vertex vi and again at vertex vj. Thus we're counting each edge exactly twice, which gives us 2E, the right-hand side of the above formula. Q.E.D.
Exercise: Use the same argument to show that if f1, f2, ..., fm are the faces of a planar graph G, then
So what does this tell us about the Platonic solids? Well, remember that each Platonic solid must have each face be the same regular polygon, which means that each face has the same degree. Also, each vertex will have the same degree. (Hmmm ... does that need a proof, or do we already know this? Hmmm...). Thus the previous Theorem tells us that if V is the number of vertices in a Platonic solid and F is the number of faces, and if each vertex has degree d and each face has degree k, then
There are lots of things we could do with this! For example, we could write these as V = (2/d)E and F = (2/k)E, and then plug them into Euler's Formula to get
So go ahead! Use (d-2)(k-2)<4 to see if any other cases of d and k are impossible, and for the ones that are possible use (2/d + 2/k - 1)E = 2 to compute how many edges the Platonic solid must have, and then use V = (2/d)E and F = (2/k)E to compute the number of vertices and faces. You should recognize the numbers that you get (is one the cube? is one the octahedron? etc) and in this way prove that there are only 5 possibilities for the Platonic solids.
Return to Combinatorial Geometry Page