|
MA 323 Combinatorial Geometry Let's now go on what will seem like a detour: let's review what we learned about linear transformations in the plane from Linear Algebra. To be brief, recall that any linear transformation of the plane must be one of the following types: Translations: These are where we shift everything in the plane over by some fixed vector (a,b). In other words, every point (x,y) in the plane gets moved to the point (x+a, y+b). It's often useful to express such transformations as vector or matrix operations. A translation would look like this:
Dilations (or Scaling): These are when you want to shrink or expand everything in the plane by some amount. Usually, to make the operation more simple, we assume we are shrinking or expanding with the origin at the center. There are two ways we could express dilations. We can use vectors and scalar multiplication:
Here c is the number we are contracting by: If c=1 there is no change. If c<1 then (x,y) will move closer to the origin. If c>1 then (x,y) will move further away from the origin. We can also use a matrix to do this same thing:
Rotations: We can also rotate the plane by some angle q. An operation line this must by expressed by a matrix. It can be fun to derive the matrix yourself, but here’s the standard matrix for rotating the plane about the origin by angle q:
So wait, what if you wanted to rotate the plane about some point other than the origin? Simple! You can compose linear transformations to do things like this. So suppose you wanted to rotate by q about the point (c,d). First you translate (c,d) to the origin (that is, translate by (-c,-d) ), then rotate by q, then translate by (c,d) to put the center of rotation back where it should be. This is what the matrix operations would look like:
(See? You subtract c from x and d from y before multiplying the rotation matrix. Then you add c and d back in.) Reflections: Reflections are wild, and will be very useful to us in origami. A reflection the operation that reflects, of flips the entire plane about a given line. For example, if we reflected everything about the y-axis, an arbitrary point (x,y) would go to (-x,y). Look at how you would represent this as a matrix operation:
To reflect about the x-axis, you’d use a similar-looking matrix:
Exercise: Find matrices that will
Exercise: Find a general matrix for reflecting about a line y=mx. You might want to think about this as first rotating the line y=mx to the x-axis, THEN reflecting about the x-axis, THEN rotating the line back into its original position. There are also things called glide reflections, which are like a reflection composed with a translation, and other things called skews, but I'll skip those since they don't relate to what we're really interested in... Reflections and Origami Now, what does all this have to do with paper folding? Well, if we have a piece of paper, and we make a straight fold, all the way across, then half of the paper has been reflected to the other side, right? So we can think of folding (flat folding, at least) as being a reflection.
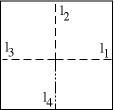
So, what can we do with this new insight? (Actually, it's not that new; Justin and Kawasaki seem to have been the first to think about origami in this way.) One thing we can do is introduce some notation! Let R(li) denote the 2 x 2 matrix that reflects the plane about the line li. Exercise: Consider the most simple flat vertex we can make: folding a square in half and in half again. (That is, four crease lines at right angles to each other. See the below picture.)
Your task is to:
The punchline here is that we should be able to use reflection matrices to model paper folding. That is, instead of talking about the angles between creases (like we did in Kawasaki's Theorem), why not just think of the creases as being fixed in the x-y plane and reflecting about them every time we make a fold? Might we be able to get results on flat origami using this approach? The above exercise should give you one possible answer to this question...
Part 2 of Foldings are Reflections Return to Combinatorial Geometry Page |