MA 323A Combinatorial Geometry!
Notes on Making Tori
via Modular Origami

The word torus is the mathematical term for donut. These notes describe how one can construct tori using the PHiZZ Unit.
You may be confused, because throughout my notes on Buckyballs I only discuss making pentagon and hexagon rings out of PHiZZ Units. I assert that making square or (shudder!) triangle rings is very awkward, if not impossible (it really depends on what kind of paper you're using) with the PHiZZ Unit. However, making larger rings is entirely possible, yet this will force the ring to "get bendy." In other words, unless you add extra creases to the units, the ring will not lie in a plane.
Exercise: Why is this true? Why will a hexagon ring lie nicely in the plane, yet a (for instance) heptagon (7-sided) ring won't when made from PHiZZ Units?
The technical term for what's going on here is that rings made from PHiZZ Units with more than 6 sides must introduce negative curvature into the surface of the object that you're making. (Whereas pentagon rings gave us positive curvature and hexagon rings give us zero curvature.) If you think about it, we need such negative curvature to make the "inside part" of a torus. This is because if you're a large ant walking on a donut the surface will feel like the surface of a sphere while you're walking on the outer part of the donut. But when you try to walk through the hole the surface will "feel" like the surface of a 3D saddle point. That's the negative curvature!
So, to make a modular torus out of PHiZZ Units (or any other origami units, for that matter) you'll need to put things like pentagons along the "outer extremity" of the torus to give it positive curvature, and you'll need either heptagon or octagon or other n-gon rings (with n>6) along the "inner extremity" to provide the negative curvature. In between these rings you'll need hexagons to make the rest of the torus.
I first made a torus from PHiZZ Units in May, 1999, and I displayed it at the 1999 OrigamiUSA Annual Convention. You can see a picture of what it looked like under construction HERE. It requires 660 PHiZZ Units and had 10 pentagon and 10 heptagon rings. (And a whole bunch of hexagons!) Soon afterward, Roberto Gretter of Italy made one of his own, which can be seen on his origami web page. His ended up being structurally different from mine, requiring only 555 units, but still having 10 pentagons and 10 heptagons.
Actually, you can prove that if you restrict yourself to just pentagons, hexagons, and heptagons, then there must be an equal number of pentagons and heptagons. This is the same kind of combinatorics at work that forces all Buckyballs to have exactly 12 pentagons.
In fact, you can prove it the same way, using Euler's Formula. However, Euler's Formula only works on the sphere, or on planar graphs, right? Polyhedra that take the form of a torus can not be turned into planar graphs. But Euler's Formula can be modified to still apply to polyhedra and graphs drawn on the surface of a torus; it becomes Euler's Formula for the Torus:
Theorem: When making a torus out of PHiZZ Units using only pentagon, hexagon, and heptagon rings, the number of pentagons and the number of heptagons must be equal.
Proof: Since we're using PHiZZ Units, each vertex of our torus will have degree 3. If we use the old "count the number of edges adjacent to each vertex" trick, we get 3V = 2E, which we will write as V = (2/3) E. Plugging this into V-E+F=0 gives us F - (1/3) E = 0, or
Let f5, f6, and f7 be the number of pentagons, hexagons, and heptagons in the torus, respectively. Thus we have f5 + f6 + f7 = F. Also, if we do the counting trick where we go to every face and count the number of edges going around it, we get 5f5 + 6f6 + 7f7 = 2E, since we count each edge twice when doing this. Plugging each of these into 6F-2E=0 gives
So, f5 - f7=0
And therefore f5 = f7, as was to be shown. Q.E.D.
Exercise: If we used only pentagons, hexagons, and octagons what would the relationshiop between the number of pentagons and octagons be? How about if we used only pentagons, hexagons, and n-gons, where n>6?
This is very useful information, but it doesn't help you actually plan out how to made one of these tori. Roberto Gretter, on his web page linked above, provides a drawing schematic of the structure of his 555-unit torus. This can be used as a "road map" for making a torus of your own. Below I provide a "road map" for making a 240-unit torus. To see how these road maps work you need to understand the concept of drawing the fundamental domain of a torus.
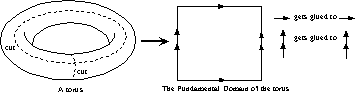
If you imagine a torus being "cut" along two perpendicular lines, one going lengthwise around the donut and one through the hole, as shown above, then you can unwrap the torus into a flat square or rectangle. This provides an easier way to draw "on" a torus, as long as we remember that the edges of the rectangle must be identified to make the torus whole again. That is, anything that is drawn to the top edge must "come out" at the bottom edge, and everything that is drawn to the left side must come out the right, and vice-versa. (It's as if you were playing the old-time video game Asteriods.) This rectangle is often called the fundamental domain of the torus.
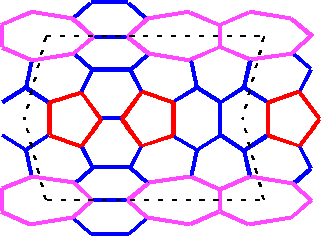
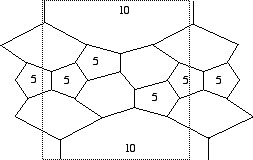
Above is drawn the fundamental domain of the 240-unit torus that I made. (It's basically Roberto Gretter's design with fewer hexagons.) Notice that there are only two pentagons shown in this fundamental domain. This is because we think of this domain as being "tiled" on the surface of the torus, in this case it gets tiled 5 times around the donut. This gives us a total of 10 pentagons and 10 heptagons. But the number of hexagons in this torus is smaller than in my first torus or in Roberto Gretter's. That's why we get fewer units.

As of this writing (4/30/00) I haven't been able to make a smaller torus out of PHiZZ Units than one using 240 units. If you manage to make one, please let me know!
Now, one could make tori with more than one hole as well! A torus is said to have genus g if it has g holes. Euler's Generalized Formula for Sufraces with Genus g is V - E + F = 2 - 2g. Give it a shot! Try making a 2-holed or 3-holed torus!
Update on 5/5/00:
My next project in this vien is to make a genus 2 torus. One could view this as just a 2-holed torus, but there's another, topologically equivalent way you could draw such an object: you take a torus and attach a BIG handle to it at opposite "ends".In any case, making this with PHiZZ units would require a "Y junction" shown below:

Exercise: Why did the number of pentagons and heptagons come out the way they did in this model? What's the relationship I'll need for my complete genus 2 surface?
Update on 6/18/01:
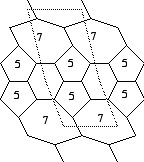
I know, I know, this is REALLY late update, but I was cleaning up some files recently and came across the following picture. It shows two tori that are MUCH smaller than the ones described above.Indeed, at the 2000 HCSSiM (Hampshire College Summer Studies in Mathematics) program I challenged several of the kids to develop PHiZZ unit tori that use fewer than 240 units. I figured that smaller tori must be possible, but I hadn't sat down to try making any. Sergei Lupashin came up will the following, rather tricky fundamental domain:
Then one of my fellow HCSSiM instructors, sarah-marie belcastro, came up with another, very graceful fundamental domain:
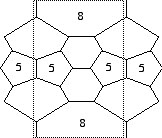
This one has only pentagon, hexagon, and octagon faces! Using octagons instead of heptagons changes the combinatorics slightly. (Exercise: Prove that with only pentagons, hexagons, and octagons you'll need twice as many pentagons as octagons!) This fundamental domain turns out to be very flexible! You can tile it 5 times to make a very nice torus, requiring 105 PHiZZ units, or you can tile it 4 times (84 units), or you can tile it 3 times (only 63 units)! The 3-tiled version is quite difficult; the units stretch a lot, and if the paper you use is too slippery then it'll likely fall apart. In fact, below is a picture of a 5-tiled version and a 3-tiled version:

(This picture was taken in August 2000 in the classroom of the "Origami Geometry" workshop I taught at HCSSiM, Hampshire College, Amherst, MA.)
In the spirit of such explorations, I came up with a fundamental domain of my own:
Some people made tori that were a little smaller (I think the smallest so far has been 60 or 48) using 12-gons, but the ones that I saw like this were pretty warped and didn't look too much like tori. Still, feel free to come up with your own!
Return to Combinatorial Geometry Page