|
Project Origami
NEWS! (11/22/2012) A second edition is coming out! See details below!

Hello! If you're visiting this web site, then you must be interested in my Project Origami book.
This book is a workbook of in-class projects that you
can insert into various college- or high-school-level math classes. (Some might be appropriate
for middle-school classes.) Each project includes a brief description,
handouts, solutions, and follow-up ideas. Most of these projects I've
used myself in classes years ago at Merrimack
College and more recently at Western New England University. All of them were, collectively, beta-tested by over 30 college and university mathematics professors from around the country.
The idea is that origami is an active, hands-on way to engage students
directly with mathematical concepts. Origami not only offers an easy
way to inject active-learning into your classes, but it's also a fertile
field for discovery-based learning. Furthermore, it's amazing how many
different mathematical topics can turn up in paper folding. Students
will be amazed to see how the math topic they are studying actually
has applications in, of all places, origami!
News on the 2nd edition:
Since this book came out in 2006, I've made a bunch of new origami activities, many of which were inspired by my own students. Also, several errors in the book were pointed out to me by various people. It seemed the time was right for a 2nd edition of the book.
The 2nd edition contains 8 new activities and about 100 new pages of material. (That is, the book is now 1/3 bigger!) In the below table of contents, the activities marked with asterisks * are new.
But many of the previous activities were either updated, had minor errors corrected, or were extensively revised. In particular, the Five Intersecting Tetrahedra activity was drastically re-done, correcting a major flaw, presenting the mathematical component in a more simple way, and a more elegant solution provided. On the whole, I think this edition is a substantial improvement on the previous one.
Below is a list of the activities in the book (an informal table of contents) along with a brief description. The CRC Press web page for the second edition lists it as being available on January 9, 2013. Yup!
The Projects:
Folding Equilateral Triangles in a
Square (geometry, calculus)
This asks, "How do you fold a perfect, equilateral triangle in
a square piece of paper? And how do you make it as big as possible?
*Origami Trigonometry
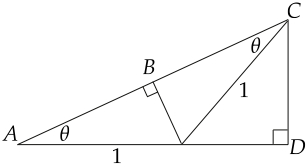 (trigonometry, precalculus)
(trigonometry, precalculus)
Paper-folding methods are explored that (a) prove the double-angle formula for sine and cosine and (b) can determine trig values of non-standard angles, like 15 degrees and 22.5 degrees.
Dividing a Length into nths: Fujimoto
Approximation (calculus, number theory, discrete dynamical systems,
modeling)
This is a really cool way to approximate dividing the side of a square
into n equal pieces. It can either be a simple example of error converging
to zero in calculus, or a wild application of number theory, depending
on how much you do.
Dividing a Length into nths: Exact
Methods (geometry, precalculus)
Using simple precalculus methods, students can see how to divide the
side of a square into perfect 3rds via paper folding. Or 5ths, 7ths,
etc.
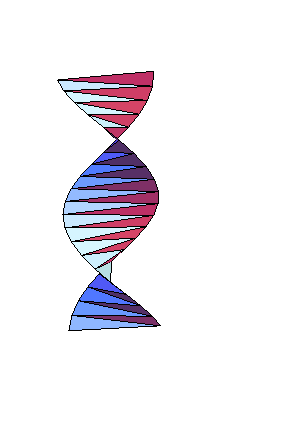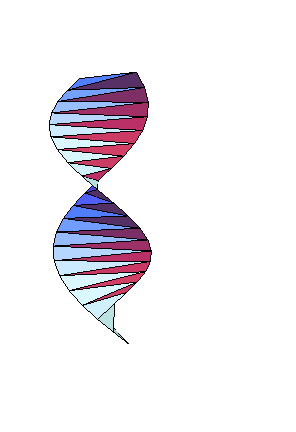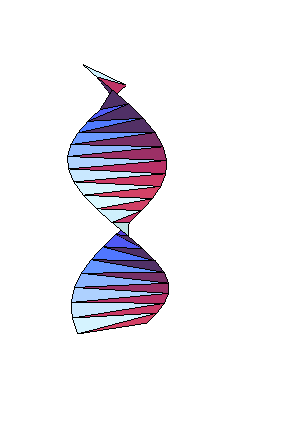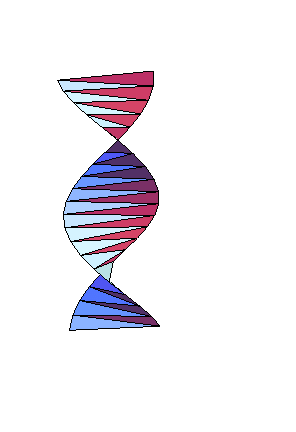
*Origami Helix
(trigonometry, precalculus, calculus, geometry)
An origami helix is folded that leads to an exercise involving sinple geometry, radian angle measure, and possibly L'Hopital's Rule from calculus.
Folding a Parabola (geometry,
precalculus, calculus, abstract algebra, modeling )
This can be an easy calc or precalc exercise on folding tangent lines
to a given parabola. Or it can be an example of how performing geometric
operations can be equivalent to solving algebraic equations. Field theory,
anyone? This one is also born to be done on Geometer's Sketchpad.
Can Origami Trisect an Angle?
(geometry, abstract algebra)
The answer is YES!
Solving Cubic Equations (geometry,
abstract algebra)
Yes, origami can solve general cubic equations, and I have an activity
here that demonstrates this. This is another one that's great to use
with Geometer's Sketchpad.
*Lill's Method
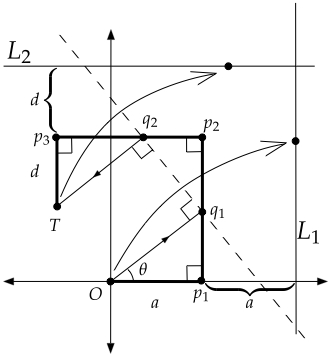 (geometry, abstract algebra)
(geometry, abstract algebra)
I little-known (but amazingly simple) geometric method to find real roots of polynomials is shown, the cubic case of which can be performed via origami. This gives a hands-on way for students to really see that origami can solve cubic equations.
Folding a Strip into Knots (geometry,
number theory, abstract algebra)
It can be wild fun to tie a strip of paper into a flat, regular pentagon-shaped
knot. But can we also make hexagon knots, heptagon knots, etc? Amazingly,
this can be translated into a problem involving the Euler phi function.
And if we allow ourselves to use multiple strips of paper, we get a
great appplication of cosets! (Of all things!)
Haga's "Origamics"
(geometry, math for liberal arts, intro to proof )
These are very creative little exercises that explore the intrinsic
geometry of paper as we fold it. They require no previous knowledge
of ANYTHING and offer loads of chances for discovery-based conjecturing
and proofing.
*Modular Star Ring
(precalculus, geometry, math for liberal arts)
I simple modular unit is presented that makes a star-shaped ring. The question is: How many units should be made to make the ring fit perfectly together?
Folding a Butterfly Bomb (geometry,
math for liberal arts)
This is a tricky model to put together, but when you're done you can
toss it in the air, wack it, and it'll explode in a shower of paper!
Building this requires learning about the structure of the cubeoctahedron.
*Molly's Hexahedron
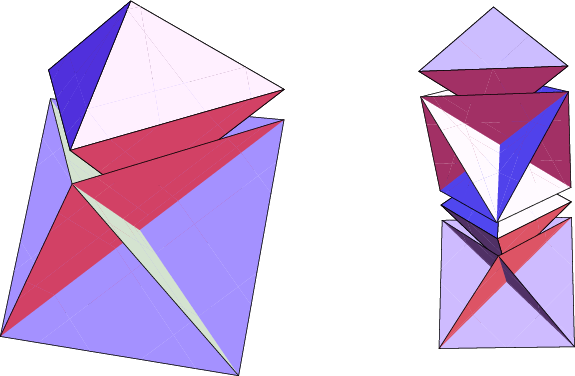 (precalculus, geometry, math for liberal arts)
(precalculus, geometry, math for liberal arts)
This is a very simple, three-piece modular that makes an interesting hexahedron shape. Students are asked to calculate the volume of this solid, assuming that we started with square pieces of paper with side length one. The answer might be a little surprising and can lead to discussions on how to dissect the cube in interesting ways.
Business Card Modulars (geometry,
math for liberal arts)
This VERY simple module is made from standard business cards. Two of
them make a regular tetrahedron. Four make an octahedron. Ten make an
icosahedron. Six can make a snub disphenoid. (Ha!)
Folding Five Intersecting Tetrahedra

(geometry, math for liberal arts, vector calculus)
The units of this
model are easy to make, but putting it all together is a real puzzle.
Building this stunning model offers a chance to study numerous symmetries
of the dodecahedron. And exploring the specifics of this model is a
challenging vector calculus project.
Making Origami Buckyballs 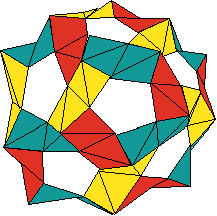 (geometry,
graph theory) (geometry,
graph theory)
This includes instructions for my PHiZZ unit which is very good at making
geodesic dome structures. Lots of graph theory to explore here (assumes
knowledge of Euler's formula).
Making Origami Tori (geometry,
graph theory, topology)
The PHiZZ unit can make "Bucky tori" too! Planning these kinds
of structures requires messing around with tori fundamental domains
and Euler's formula for the torus.
Modular Menger's Sponge (fractal
geometry, discrete math, combinatorics)
In a fractals course, this is a way to easily build iterations of this
fractal. But the combinatorial questions that arise (basically, how
many business cards will we need to make a Level n sponge?) can involve
recurrence relations and generating functions.
Folding and Coloring a Crane
(discrete math, graph theory)
The mathematics of flat origami models, like the classic crane (or flapping
bird) actually leads to some fun questions on graph colorings.
Exploring Flat Vertex Folds
(geometry, discrete math, combinatorics, math for liberal arts, intro
to proof, modeling)
This open-ended, discovery-based project can give students at all levels
a taste of what mathematical research is like. The students play with
paper, make conjectures, and try to prove them.
Impossible Crease Patterns (geometry,
discrete math, combinatorics, math for liberal arts, intro to proof,
modeling)
A follow-up to the previous activity, students are asked to fold up
crease patterns that are given to them. Ooops! They are impossible to
fold flat! The question is why...
Folding a Square Twist (geometry,
discrete math, combinatorics, math for liberal arts, intro to proof,
modeling, abstract algebra)
This little fold is one of the most counter-intuitive ways in which
paper can fold flat. The question asked is, "How many different
ways can we fold this up?" Approaches to this can utilize either
brute force, combinatorics, or Burnside's Theorem.
*Counting Flat Folds
(combinatorics, geometry, discrete math)
Given a few degree-four flat vertex folds, students are asked to count the number of different ways in which they can fold flat. The patterns gleaned from these examples can then be used to generate upper and lower bounds for the number of ways to fold a generic origami vertex flat.
*Self-similar Wave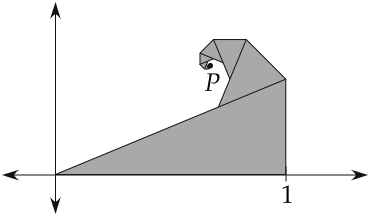 (geometry, fractals, complex analysis)
(geometry, fractals, complex analysis)
An origami model is taught whose crease pattern is self-similar and that results in a spiral shape that looks like an ocean wave. An interesting exercise is to set up a coordinate axis for the folded model and calculate the convergent point of the spiral. This can be done either with affine transformations or complex numbers. A side-question is whether or not such a model is an actual origami fractal.
Matrix Model of Flat Vertex Folds
(geometry, linear algebra, modeling)
Let's face it–when we fold a piece of paper in half, we're actually
reflecting half of the paper. So folding flat is really doing a reflection.
Thus we should be able to model flat paper folding using reflection
matricies. What can we do with these matrices?
Matrix Model of 3D Vertex Folds
(geometry, linear algebra, modeling)
For that matter, even when we fold a piece of paper in a non-flat manner
(leaving a dihedral angle in the paper), we can still use a matrix model–but
now we need to use 3D rotation matrices! This gets much more confusing
and really tests students' knowledge of matrix operations and 3D rotation
matrices.
*Origami and Homomorphisms
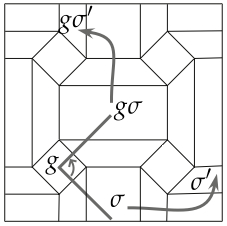 (abstract algebra)
(abstract algebra)
This is a very challenging (but valuable) activity where students who have learned about homomorphisms in group theory can see how they can be used to calculate the symmetry group of a flat origami model given the symmetry group of its crease pattern. Seriously!
Rigid Folds 1: Gaussian Curvature
(geometry, differential geometry)
How can we model rigid paper folding? That is, if we used sheet metal
instead of paper and hinges instead of creases, could we still fold?
The matrix model gives one way to look at this, but it only tells us
about the finished folded state, not how we got there. Gaussian curvature
can help us fill in the blanks.
Rigid Folds 2: Spherical Trigonometry
(geometry)
By wading through some messy trig and the spherical law of cosines,
we end up with a powerful theorem about the dihedral angles in 4-valent
rigid folds as they open and close. This can tell us when some multiple-vertex
crease patterns won't be rigidly foldable.
Questions? Comments?
Email me: thull@wne.edu
Thanks for visiting!
Last updated: 11/22/2012 |
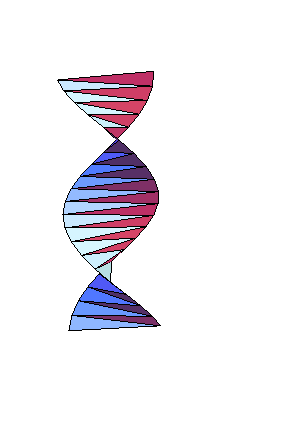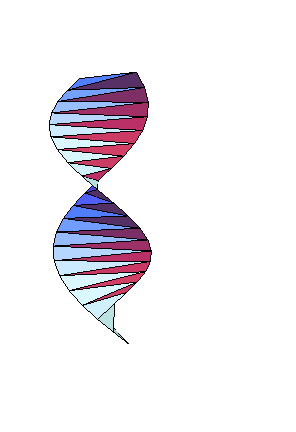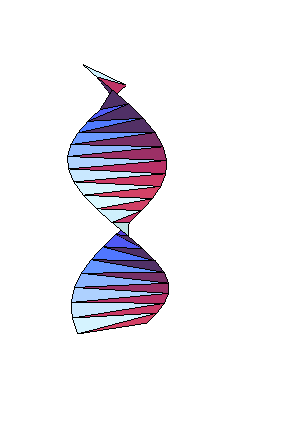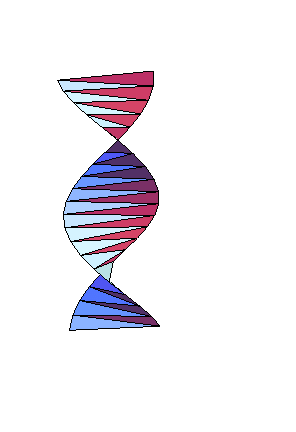
 (trigonometry, precalculus)
(trigonometry, precalculus) (geometry, abstract algebra)
(geometry, abstract algebra) (precalculus, geometry, math for liberal arts)
(precalculus, geometry, math for liberal arts)
 (geometry,
graph theory)
(geometry,
graph theory) (geometry, fractals, complex analysis)
(geometry, fractals, complex analysis) (abstract algebra)
(abstract algebra)