Lately I've had a hankerin' to make an origami version of the classic
compound of three octahedra.
The construction of this model is still under development, so for now
I'll just describe
what the object is and how I'm trying to go about making one.

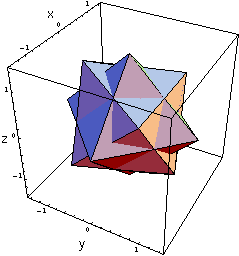
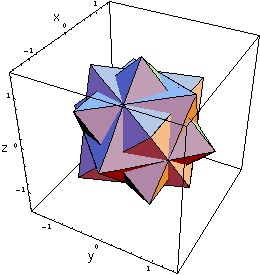
To make an origami version, I'm trying to use the same strategy that I used for the compound of five tetrahedra (i.e., five intersecting tetrahedra, FIT), where one makes polyhedral frames to represent the polyhedra. With the FIT this was ideal, since the edges of the tetrahedra never intersected each other and thus the tetrahedral frames wouldn't intersect either, provided they were thin enough. But in this object, the edges of different octahedra do intersect (in two different ways, at that). So the frame approach would have to take this into account. To handle this, I chose to modify things slightly. In the FIT model the edges of the frames are made from units whose cross section, when locked together, makes a 60° wedge. If I wanted to do this with the compound of three octahedra, I'd have to compute all the different angles at which the sides of different octahedra intersect, and have different units for each of these situations. What a pain! So instead I chose to have the cross section of the edge units be flat, that is, a 0° angle. This will handle any angle at which the edges intersect, provided that in the case where more than 2 edges intersect, they all intersect in the same plane. I've made a modification to Francis Ow's unit to do just this. The next problem was computing how long the various edge segments had to be. Once you start thinking about this object as three octahedra rotated at different angles, these lengths are fairly easy to compute. As of this writing, I've made one such model. I'm still working on producing a graphic of what the final object looks like, but I am also forced to admit that this procedure did not work as amazingly as I had hoped. All the different types of intersection, together with the ever-present fudge error, not to mention the physical reality that the units are not completely flat (they weren't very willing to make a perfect 0° angle for me), combined to produce a lot of strain on the model during the assembly process. Thus the whole thing was quite difficult to put together. Perhaps some modifications are in order to better achieve this marvelous object. Keep checking this page for more info as I pursue this design! Update: I've let this project slip by for a very long time. (The above page was written in 1997, and I'm updating this now in 2008!) But Daniel Kwan found some interesting ways to solve this problem. I first saw a version of three intersecting octahedra that he had folded in an exhibit of his at the OrigamiUSA Annual Convention in 2002 or thereabouts. But you can also see a verion of his solution on Daniel Kwan's flickr photo page where he has lots of other cool models besides. |