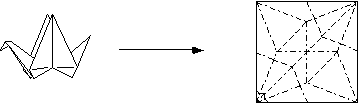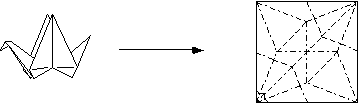Origami Mathematics
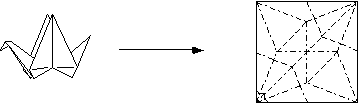 These pages are an attempt to begin collecting information on the
mathematics of paper folding. Anyone who has practiced origami has
probably, at one time or another, unfolded an origami model and marveled
at the intricate crease pattern which forms the "blueprint" of the fold.
Clearly there are some rules at play in these collection of creases.
Clearly there is an origami geometry at work when paper is folded.
These pages are an attempt to begin collecting information on the
mathematics of paper folding. Anyone who has practiced origami has
probably, at one time or another, unfolded an origami model and marveled
at the intricate crease pattern which forms the "blueprint" of the fold.
Clearly there are some rules at play in these collection of creases.
Clearly there is an origami geometry at work when paper is folded.
Such geometry, this mathematics of origami, has been studied extensively
by origamists, mathematicians, scientists and artists. The
Italian-Japanese mathematician Humiaki Huzita has formulated a list of
axioms to define origami geometrically. Physicist Jun Maekawa has
discovered some fundamental theorems about origami and used them to
design origami models of surprising elegance. Mathematician Toshikazu
Kawasaki has a number of origami theorems to his name and has even
generalized some of them to describe paper folding in higher dimensions.
(Origami in the fourth dimension!) Robert Lang of California has
developed an ingenious way to algorithmatize the origami design process,
using a computer to help him invent models of amazing complexity.
Educator Shuzo Fujimoto and artist Chris Palmer have discovered amazing
parallels between origami and tessellations. And an enormous number of
teachers have been developing ways to use origami to teach concepts in
math, chemistry, physics and architecture.
Unfortunately, much of the above-mentioned work is new, and at the time
of this writing there are few good references for this type of
information. These pages will try to help solve this problem by
providing an
extensive bibliography for origami-math, list upcoming lectures and
events, and offer instructions and tutorials for select topics.
However, this is an on-going project! These pages are still in their
infancy, and any comments or suggestions (or offers to help!) would be
greatly appreciated!
Origami Math Menu:
- Browse our Origami Math
Bibliography, which includes references to a few recent books on origami-math.
- Science Fair and Project Advice
Looking for ideas for a science fair or class project on origami math? Look here before emailing me.
- My YouTube Channel
This doesn't have much math on it (yet), but I have placed some videos there that teach some of my more recent geometric modular models.
- Tutorial: Origami Geometric
Constructions
We present Humiaki Huzita's origami axiom list and compare this to
traditional straight edge and compass constructions. Instructions for
trisecting angles and doubling cubes are also included.
Note: This section is badly out-of-date. I need to update it.
- Rigid Origami
If a piece of paper were made out of sheet metal with hinges instead of creases, it would still fold up? This is a very brief discussion of this problem.
- Rigid Folding of a Tetrahedron
You can't rigidly fold up a tetrahedron (since that would violate the bellows theorem). But what if you make a small slit in the tetrahedron? Then you can do it!
- Triangular Rigid Fold with a Locked State
Some people thought that if you had an origami model that doesn't fold rigidly, then you could make it rigidly-foldable by adding creases to make each face of the crease pattern be a triangle. This usually works, but not always! The example we show here is a crease pattern with all triangle faces and that has a "locked folded state" from which it cannot be unfolded rigidly!
- Rigid Folding of the Augmented Square Twist
This is work with a student of mine, Michael Urbanski, at Western New England University (done in 2017-2018). It looks at a way to make the classic square twist rigidly foldable!
- Model: Five Intersecting
Tetrahedra

- Model/Tutorial:
Pentagon-Hexagon Zig-Zag (PHiZZ) Units
- Origami Model Gallery
- Model: Compound of Three
Octahedra
under construction!
-
Notes for an Origami/Combinatorial Geometry Course
These are notes and assignments for a course at Merrimack College on
combinatorial geometry. The main application covered in this course
is the mathematics of paperfolding.
- There's a great article (PDF format)
by Barry Cipra in the Oct. 2001 issue of SIAM News. Barry reports on the 3OSME
conference, but the article summarizes a lot of origami math, design, and
applications very well. Check it out!
- Other Origami Math
Pages
These pages Copyright 1997-2015 by Thomas Hull.
Last changed 3/14/15.