Plenary Talks     Mathematics of Origami     Origami in Education   Science and Applications
 

Plenary Talks

Energetics of Crumpling
Brian DiDonna (University of Chicago)

Abstract: When a thin sheet of elastic material is confined within a shrinking volume it does not deform uniformly, but instead forms a network of singular point and ridges. This crumpling process can be viewed as a condensation of elastic energy onto the area surrounding ridge lines, an area fraction of the sheet which becomes arbitrarily small as the thickness of the sheet goes to zero.  The energy condensation is driven by a competition between bending and stretching energy costs, which are coupled by the geometric relation between curvature and strain.  In this lecture I will review the energy scaling properties of  ridges in thin elastic sheets. I will then present the results of our studies on crumpling of thin sheets in four spatial dimensions.  Changing the spatial dimension changes the geometric coupling between energies.  In simulations of very thin sheets in 3 or 4 spatial dimensions, small deviation of the sheet into the fourth dimension effectively negated the strain field around ridges - leading to greatly reduced total elastic energy and  different energy scaling. I will discuss whether  the two cases converge to the same configuration in the unstretchable limit. I will also comment on the insights this research gives into the nature of singularities in regular crumpling.

For more information and illustrations, go to  http://vonkarman.uchicago.edu/gallery/.
 

Fold Paper and Enjoy Mathematics: ORIGAMICS
Kazuo Haga (University of Tsukuba, Japan)

Abstract: The subject of our meeting ORIGAMI is an international word which is derived from the Japanese word origami.  They have same spelling, but they differ somewhat in sense as well as pronunciation.  The accent of the former falls on the third syllable (ga) while the latter on second one (ri).  In Japan, origami usually means a handicraft hobby for children, so almost all books about origami are arranged in the juvenile section of bookstore even if some of them are for enthusiasts.
    Regarding above circumstances, I felt the need for a new name to describe the genre of scientific origami other than origami for children. I was motivated in this during the 1980s after finding several mathematical phenomena in folded square paper.  I finally proposed the term
ORIGAMICS at the 2nd Origami Science Meeting in 1994 for studies upon my findings.  The term is made of the stem, origami and the suffix, ics which is often used to stand for science or technology, as mathematics.  Now I think that the term ORIGAMICS may become a good name to represent all scientific origami shown at 3OSME.
    I will talk about some origamics phenomena below which appear on a simply folded square or rectangle sheet of paper.  Please fold paper together with me and experience my origamics world!
    #1  The first step of folding induces an insect face pattern.
    #2  Haga's theorem enables a standard rectangle paper to divide its length into an odd number of equal parts.
    #3  An arbitrarily made mother line bears eleven wonder babies.
    #4  How to fold a mathematically accurate pentagram star from a single sheet of square paper.
 
 

The Mathematics of Origami
 

Mathematical Origami  and Alhazen's Problem
Roger Alperin (San Jose State University)

Abstract: I will give a survey of the axioms of mathematical origami and their connections with the theory of fields and constructions with conics. I will illustrate how to use the algebraic information from fields and curves to construct a solution to the famous optical problem of Alhazen and indicate how this leads to a solution by origami.
 

Origami and Origami Numbers
Kazuo Amano (Gifu University, Japan)

Abstract: The art of origami is from Japanese traditional culture and produces many interesting geometrical shapes. In the present paper, we study which shapes are possible to construct using origami. Then we obtain the necessary and sufficient condition for which a real number is an origami number constructed by origami. Also, a regular polygon of p (p:odd prime) sides can be constructed using origami if and only if p is an origami prime. Those were described by H.Huzita and B.Scimeni in the Proceedings of the First Meeting of Origami Science and Technology, but our proofs are different from theirs. In our proofs, the trisection of an angle by H.Abe, the duplication of the cube volume and the Cardano's formula of the cubic equation play essential parts. Moreover, we study two classical construction problems of Pappus and Philo. It is impossible to construct these problems using a compass and straight edge, but we can solve these problems using origami.
 

Computational Tools for Origami Tessellations
Alex Bateman (The Sanger Centre, UK)

Abstract: There are currently very few computer applications specifically written for origami. The most notable example is TreeMaker by Robert Lang, which allows design of complex bases for origami.
  To date no software exists for the design of origami tessellations.  Here I present a program for designing tilings of a plane, which can then be used as the basis for origami tessellations. The program generates crease patterns from tilings and a representation of the final folded form, allowing rapid design of new complex origami tessellations.
  There exist very few instructions for making origami tessellations, it is expected that this software would make this style of origami more widely accessible.
 

Modelling the Folding of Paper into Three Dimensions
sarah-marie belcastro (University of Northern Iowa), Thomas Hull (Merrimack College)

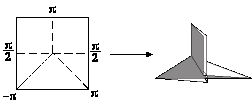
Abstract:  We model the folding of ordinary paper via piecewise isometries from R^2 to R^3.  The collection of crease lines and vertices in the unfolded paper is called the crease pattern; we mainly consider the case of crease patterns with a single vertex.  Our results generalize the previously known necessity conditions from the more restrictive case of folding paper flat (into R^2); if the crease pattern is foldable, then the product (in a nonintuitive order!) of the associated rotational matrices is the identity matrix.  This condition holds locally in a multiple vertex crease pattern and can be adapted to a global condition.  Sufficiency conditions are significantly harder, and are not known except in the two-dimensional single-vertex case.  We have achieved partial results in this arena.
 

The Complexity of Flat Origami
Marshall Bern (Xerox PARC), Barry Hayes (Placeware Inc.)

Abstract: We study a basic problem in mathematical origami: determine if a given crease pattern can be folded to a flat origami. We show that assigning mountain and valley folds is NP-hard. We also show that determining a suitable overlap order for flaps is NP-hard, even assuming a valid mountain and valley assignment.
 

A Disk-Packing Algorithm for an Origami Magic Trick
Marshall Bern (Xerox PARC), Erik Demaine (University of Waterloo), David Eppstein (University of California - Irvine), Barry Hayes (Placeware Inc.)

Abstract: We present an algorithm for a magic trick. Given a polygon with holes P, our algorithm determines a folding of a rectangular sheet of paper such that a single straight cut suffices to cut out P.
 

Recent Results in Computational Origami
Erik D. Demaine Martin L. Demaine (University of Waterloo)

Abstract: Computational origami is a recent branch of computer science studying efficient algorithms for solving paper-folding problems.  This field essentially began with Robert Lang's work on algorithmic origami design, starting around 1993. Since then, the field of computational origami has grown significantly.  The purpose of this paper is to survey the work in the field, with a focus on recent results, and to present several open problems that remain. Along the way, we present some new related results.
    One body of work studies what is possible by folding paper, and designing an algorithm to find those foldings.  For example, any tree-shaped origami base, any polygonal silhouette, and any polyhedral surface can be folded out of a large-enough piece of paper.  Not all folding problems have efficient algorithms.  For example, it is computationally intractable (NP-hard) to tell whether a crease pattern folds into any flat origami, even when folds are restricted to simple folds.  Other topics we explore include unfolding polyhedra, flattening polyhedra, and map folding.
 

Just Like Young Gauss Playing with a Square: Folding the Regular 17-gon
Robert Geretschlaeger (Austria)

Abstract: When Carl Friedrich Gauss wrote about constructing a regular 17-gon with straight-edge and compass in his Disquisitiones Arithmeticae, he gave the world of mathematics a playful little morsel embedded in a work of seminal importance. Despite the fact that all straight-edge and compass constructions can readily be replaced by origami constructions, folding a regular 17-gon is not at all a simple matter if we try to follow the usual constructions. In this talk, we present a precise method of  folding such an n-gon as derived from CFG’s ideas, including all the math needed to see that the method actually must work, even if sloppy folding makes us doubt the validity of the method.
 

Counting Mountain-Valley Assignments for Flat Folds
Thomas Hull (Merrimack College)

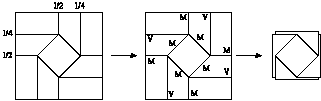
Abstract: By a flat fold we mean a finite sheet of paper that has been folded into a potentially complicated object which lies flat (can be pressed in a book without crumpling).  Flat folds can be described by their crease patterns, C, a collection of lines in the paper which indicate where the paper is folded.  A mountain-valley (MV) assignment is a function  f : C to {M,V}  which indicates which crease lines are convex and which are concave, respectively.  We examine the problem of counting the number of valid MV assignments for a given crease pattern.  In particular we develop recursive functions that count the number of valid MV assignments for flat vertex folds, crease patterns with only one vertex.  We also provide examples, especially those of Justin, that  illustrate how difficult the general, multivertex case is.
 

The Geometry of Orizuru
Toshikazu Kawasaki (Saesbo College of Technology)

Abstract: It is possible to fold the classic orizuru (crane) from paper other than a square. We can make an orizuru with long wings using rhombic paper. However, we cannot make a beautiful orizuru from a rectangle.
    Kodi Husimi thought of folding an orizuru from kite-shape paper. The details will be explained in this presentation, but it is not simple and easy to fold. To find out the method, the help of mathematics is necessary after repeated trial and error.
    Jacques Justin has generalized Husimi's study.  He argues, "It is possible to fold the orizuru from square paper if and only if it has an inscribed circle." However, Maekawa has constructed an orizuru that does not fit into the Husimi-Justin theory. We find the final orizuru theory that includes both the Husimi-Justin theory and Maekawa's  construction. This theory shows us the essence of orizuru.
 

Trees and Circles: an Efficient Algorithm for Origami Design
Robert J. Lang  (SDL, Inc., CA)

Abstract: A fundamental problem in origami of both mathematical and practical interest is the problem: given a desired folded form, construct a crease pattern in a square which, when folded, gives the initial target shape. This is a problem that is often phrased, "How do you fold a (blank)?" Surprisingly, a large class of target shapes may be folded by a deterministic process of design.  Specifically, the problem of folding any shape topologically equivalent to a tree graph that satisfies certain simple geometric conditions may be solved by a constrained nonlinear optimization and simple geometric constructions.  In this paper, I will describe the theory and the constructions and will present several examples, including a demonstration of the nonintuitive result that it is possible to fold a shape with unbounded perimeter from a finite sheet of paper.
 

The Definition of Iso-area Folding
Jun Maekawa (Maekawa Co., Ltd.)

Abstract: Origami models whose obverse and reverse sides appear identically are called "iso-area folds". The concept of iso-area folding was presented by Kawasaki, and he made iso-area cubes, iso-area octahedron and others. It is a purely geometric concept, but the definition of it hasn't been public as far as I know.

    The most general definition of iso-area folding is to regard it as a kind of "rotatory inverse symmetry" which is a concept of crystallography.  When a figure (solid) isn't changed by n (n:natural number) times rotatory inverse operation,
it is called n times rotatory inverse symmetry. The n times rotatory inverse operation means to revolve 360/n degrees and to invert by the center.
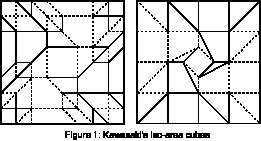
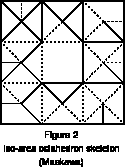
   Kawasaki made two types of iso-area cubes.  Both of them are 4 times rotatory inverse symmetry solids (figure 1).  And, figure 2 is an iso-area octahedron skeleton by Maekawa. This octahedron skeleton has different character from Kawasaki's cubes. This is one time rotatory inverse symmetry.
   The iso-area folding is equal to n (n:1 or even number) times rotatory inverse symmetry folding except 2 times. The reason why I except 2 times rotatory inverse symmetry is because it is equal to mirror symmetry and it isn't iso-area folding.
    I will show many iso-area folding models including unpublished works. And, I will refer the relation between general transform operation and origami operation (An example: replacing mountain with valley folds isn't inverse operation).
 

Perfect Bird Base From Non-square Quadrilaterals
James Minoru Sakoda (Brown University)

Abstract: There are five steps needed to take a square sheet and cut a non-square quadrilateral of one's choice and fold it into a perfect bird base as defined by Jacques Justin (ISIS Symmetry V5, No. 2, "Mathematical Remarks About Origami Bases," 153-166).
    First specify the type of quadrilateral desired, such as a kite form, a trapezoid or a combination of these by picking a location for the apex of the quadrilateral.  Second, make mountain folds from the apex to the two opposite corners and fold the shorter one toward the longer one to make a flat fold, which results in the sums of the opposite angles being equal.  Third, make a straight cut (suggested by Koji Husimi) along the edge or through layers of folds of paper to shape the desired quadrilateral.  Fourth, find the crosspoint of two hyperbolas to serve as the center of the bird base.  Fifth, fold the bird base using the preliminary fold followed by petal folds.
    The significance of the procedure is that it permits refolding of any bird base model from a family of different non-square quadrilaterals to seek changes.
 

Paper-folding Performs More Classical Constructions in Elementary Geometry
Benedetto Scimemi (Italy)

Abstract: It is well-known that some famous geometric constructions, such as duplicating a cube or trisecting an angle, cannot be achieved by ruler and compass but are successfully treated by paper-folding, provided some proper basic procedures are permitted (see e.g. Huzita, H. and  Scimemi B., The algebra of paper-folding, Proceedings of the First International Meeting of Origami Science and Technology, H. Huzita ed. (1989), 215-222).  Here we shall apply p.f. to solve other classical, though less popular geometrical problems.  As an example, we shall treat minimum problems, such as constructing a point on a given parabola whose distance from a given point is minimal, or finding a line within a given pencil which cuts a minimal length segment on two given lines (l'Huillet's problem). Other problems will regard the construction of a triangle for which a set of notable points is given or special relationships hold, regarding its perimeter, inradius etc.  While our constructions are purely syntetical and achieved by a chain of permittable p.f. procedures, their proofs will require some elementary analytical geometry.
 

Origami in Education
 

Origami as a Model for Development in Organisms
Norman Budnitz (Duke University)

Abstract:  An important field in modern biology is the study of the developmental processes in organisms.  The Human Genome Project is cataloguing the sequence of nucleotides in our DNA, but the research on the conversion of this information (the genotype), through growth and development, into an organism (the phenotype) is essential to our understanding of life and life processes.  To help students understand this morphogenesis ("form creation"), we use origami.  An origami crease pattern is the analog of the genome.  The information is there, but is generally not sufficient for producing the finished model.  Information about the folding sequence, however, makes this process much easier.  Origami models with similar, but not identical, crease patterns and folding sequences can be compared to closely related species with similar, but not identical, genomes and developmental sequences.
 

Origami in Mathematics Textbooks for Prospective Elementary School Teachers
Jack Carter (California State University), Beverly J. Ferrucci (Keene State College)

Abstract: This paper reports on a survey that was conducted on the nature and extent of paperfolding applications in contemporary United States textbooks intended for use in mathematics content courses for future primary and intermediate school teachers.
    Current reform efforts in mathematics education have emphasized the use of activity-based and hands-on instructional units to help students in their initial and informal understanding of mathematical notions.  Since origami  can be an important tool in learning symmetry and can provide unique experiences with spatial reasoning, it was expected that applications of origami would be common in the texts that were surveyed.  However, the results showed that  paperfolding activities for the prospective teachers were mostly concentrated  in the areas of intuitive geometry and geometric constructions.
    This report of the survey concludes with: (1) comparisons of the origami  applications in the texts and (2) suggestions for additional paperfolding  applications in mathematics courses for future elementary school teachers.
 

Changing Origami Directions to Mathematical Language
Beth Cipoletti (West Virginia Department of Education), Nancy Wilson (Marshall University Graduate College)

Abstract:  "Fold the paper in half."  Many origami directions include similar statements, but they are not written using mathematical language. "Mathematics generally has the reputation of having a precision that no
other subject has. . . .As teachers, we need to be aware of, and sensitive to the way we need and use language to convey our meaning" (Tappan, 2000).  It is important that educators provide "students with experiences that help them appreciate the power and precision of mathematical language" (NCTM, 2000, p. 63).Salend and Hofstetter (1996) stated that when students are offered opportunities to communicate using mathematical language their mathematical understanding improves.
    Origami, the art of paper-folding, and other types of hands-on activities increase students' ability to communicate mathematically and increase students' understanding of mathematical concepts (Fuys & Lievov, 1997; Hartshorn & Boren, 1990; Salend & Hofstetter,1996; Wohlhuter, 1998).  According to the National Council of Teachers of Mathematics, NCTM (1989, 2000), students need to investigate, explore and manipulate everyday objects to be able to describe relationships in a  multi-dimensional world using mathematical language.
    A process to rewrite origami directions to include mathematical language will be discussed.  The value of using mathematical language in origami directions in the classroom will be explored. In addition, connections between the embedded mathematics and vocabulary in origami  directions will be identified.
 

Triangular Boxes From Arbitrary Sized Rectangular Sheets of Paper: a Pedagogical Study that Incorporates Origami, Plane
Geometry, Trigonometry, and Calculus
V'Ann Cornelius (Cardiff, CA) and Arnold Tubis (Purdue University)

Abstract: The problem of designing a specific class of isosceles triangular boxes starting with single rectangular sheets of paper of arbitrary dimensions provides an interesting pedagogical example of origami, plane geometry, trigonometry, and calculus.  As such, it may be a useful source of enrichment in high school level mathematics classes.  Some aspects of the problem may also be effective for introducing informal geometric ideas in the lower grades.  The parameter space (length L and width W of starting rectangle, height of box H, and angle q  made by the two equal length sides of the triangle) is explored.  Theoretically, boxes with any specified q  may be folded, but for some parameter values, the folding would be physiologically impossible. H is determined as a function of L, W, and q . For given values of L and W, the values of theta that correspond to the maximum area of the triangular face and to the maximum volume of the folded box are determined.  The maximum area of the face of the box corresponds to q  =  90*, and the maximum box volume to theta greater than 90*.
 

Applications of Origami to the Teaching of Sophisticated Communication Techniques
Deborah Foreman-Takano, (Doshisha University, Japan)

Abstract: Apart from its well-known and successful uses in the physical and mental development of children and in specialized therapies, the learning and teaching of origami can be extremely practical for internalizing strategies and techniques necessary for successful adult communication, both interpersonal and public. It facilitates transferring the focus of attention of the interlocutor from her- or himself to the other(s) in a communicative act;  it develops consciousness of other viewpoints, other interests, and the value and methods of adapting to those variables. At the same time, it can be used to hone the development of self-presentation strategies, to enhance successful participation in communicative dyads.
    Rationales and examples will be offered of how to use origami effectively in adult communication classes of various types, including (1) EFL/ESL/comparative-culture classes and (2) classes in presentation and speechmaking.
 

Making More Use of Origami in the Elementary Classroom
Judy Hall (Westport, CT)

Abstract: In this paper the author, in her retirement, has been able to spend more time collaborating with other teachers who are also interested in using origami in their classrooms.   We look at some specific mathematical applications particularly with fractions.   We have observations of groups of children in classrooms improving their ability to get along with other classmates by teaming as they learn origami.  Another successful application has been teaching one group of children to teach others.  Self-esteem has been our goal as well as the improvement of communication skills.  Appreciating the fine art of origami is a special application we also want to have happen with students.
    Helping educators explore ways models can be adapted for their own classroom work is another way to make more use of folding.  For example, taking a rectangular box model and looking for mathematical applications can be a fresh idea for some of the new teachers in classrooms today.  Using models like this for storytelling can be another application.  Going beyond the doing of origami has been fostered by these international meetings on the science, math, education, art, and therapy using origami.  Focus groups at SEOF in Charlotte showed the interest and need for this broadening of the use of origami.
    Having more time and contacts in Connecticut, Florida, and Origami USA has enriched this educator's ability and interest in spreading the use of origami in schools.
 

Origami for Adult ESL Learners
Lillian Ho (City College of San Francisco)

Abstract: As an educational tool origami has become increasingly prominent in various disciplines such as science, mathematics, and art.  It also carries numerous benefits in physical and psychological therapy.  However, its applications in language teaching, especially for adult ESL (English as a Second Language) learners is quite nebulous. Therefore, the presenters intend to define the role of paper-folding in the teaching of ESL.  They will show how origami appeals to the kinesthetic, tactile, aesthetic, and visual styles of some learners.  They will discuss certain characteristics, unique to adult ESL teaching, that must be considered in the choice of suitable materials or techniques especially with regard to the subject of origami.  The presenters will demonstrate and explain how to create several ESL lessons using common origami models as devices to enhance the learning process.  Other sample lessons include using paper as props, creating map matrices, and diagram reading. The presenters, both skilled ESL teachers, will explain how to adapt storigami materials to adult ESL teaching.  They will show how paper can be used to elicit new or newly learned vocabulary.  There will also be a presentation of ESL activities that require the students to fold an 8 1/2 x 11 paper into parts.
 

Logic of Axiomatics in Origami Geometry
Humiaki Huzita (University of Padova, Italy)

Abstract: It is too hard for everyone to understand deeply the historical importance of the Euclidean Axioms, especially for school children and even for school teachers. I think that nowadays all the instruments necessary for the study of geometry should be easily fabricated and easy to use.  Anything less would be contrary to the intentions of Mr. Euclid, but remember that the geometry of the ancient Greeks is called called the Geometry of Ruler and Compass.
    The axiomatic origami geometry I presented many years ago illustrates the axiomatic method in a very realistic, hands-on way. Furthermore the origami geometry, contrary to others, needs not any instrument but the well known operation; folding paper.
 

To Fold or Not to Fold
Misha Litvinov (Moscow Origami Club, Russia)

Abstract: Most books on origami contain information on symbols, basic folds and elementary technique. This set of facts, in general, is quite enough for working on origami material. But for creative purposes, for satisfying natural inquisitiveness, especially with 3-dimensional origami, additional material is needed.
    It  would be very important to consider the properties of the origami nodal points, such as how a node could be folded (i.e. the number and crease patterns that are tolerable, the flatness and nonflatness of a node point). The  special features (construction, symmetry, variability, etc) of 4, 5, and 6-faced nodes are the most important elements of origami constructions. It is not too easy to visualize even just one node and the crease pattern does not help us much.
    The most effective picture of a node could be approached by a cross-section of its creases. To make this section more apparent the points of the creases should be changed  by short lines. In this case, especially if the node is flatfolded, the general scheme of the nodes becomes very clear.  The next step is to look at the foldability and flatability of  simple constructions made up of 2-3 nodal points are to  be determined, together with their symmetrical reflections.  Next, it should be determined  whether flat nodes in general origami constructions can be folded into 3-d form. These  are very complicated problems and this paper will explore what solutions can be found.
 

Reflections on a Broken Heart
Jeanine Meyer (Pace University), Aviva Meyer (Swarthmore College), Daniel Meyer (Cornell University)

Abstract: Folding, teaching and discussing origami models are mathematical activities. In this presentation and paper, the authors focus on the delightful action model "Broken Heart" by Edwin Young. A set of questions and challenges are formulated and addressed for the heart model and compared  with the preliminary and waterbomb bases.
    The questions uncover qualitive and quantitative attributes of models that change shape, relating to the nature of transformation, symmetry, dimensionality, function of folds, terminology, and diagramming. This set of questions can be applied to other action models and serve as the basis for Socratic dialogues to stimulate mathematical thinking and spatial reasoning  on the part of students.
    The Broken Heart model is diagrammed on the Meyer family origami site:  http://csis.pace.edu/~meyer/origami. (Click on Sample Models and then Broken Heart.)
 

Computer Methods to Facilitate Production of Origami Directions
Jeanine Meyer (Pace University), Aviva Meyer (Swarthmore College), Daniel Meyer (Cornell University)

Abstract: Directions for making origami models follow a more-or-less fixed methodology in most published books.  Formal diagramming, however, is not the only way to convey the procedure of making a model.
    In this presentation we will demonstrate (or teach if a computer classroom is available for a hands-on workshop) several methods for producing a variety of styles of origami directions using inexpensive, readily accessible software and hardware.  The tools include Word, Paint, Paint Shop Pro and Animation Shop, and Visual Basic. Hardware, useful beyond the computer itself, includes scanners, still cameras and digital cameras. These methods are especially appropriate for younger students for whom the production of effective directions may present great opportunities for creativity and learning.
    These methods are illustrated at the Meyer Origami page at:  http://csis.pace.edu/~meyer/origami.
 

Using Origami to Promote Geometric Reasoning and Collaboration in the Classroom
Crystal Mills, Charlene Morrow (Mount Holyoke College), Edith Kort (University of Rochester)

Abstract: This presentation focuses on the ways in which origami can serve as a context for developing mathematical ideas and insights and for posing mathematical questions. Students can explore such mathematical topics as combinations, permutations, angle measures, numerical and geometric patterns, perimeter, area, and volume relationships, the characteristics of polyhedra, symmetry, and possible map colorings.
    In geometry students often have difficulty translating the two-dimensional information on a text book page into the intended three-dimensional object. Origami can provide a useful medium for making these connections. Objects made by students themselves have great visual and personal appeal, which helps to sustain their interest in analyzing mathematical characteristics.
    We will demonstrate and discuss explicit strategies for bringing out mathematical ideas in ways that draw on the strengths of a variety of learners. 
 

Using Planar Graphs to Devise Coloring Schemes for Origami Polyhedra
Charlene Morrow (Mount Holyoke College)

Abstract: Graph theory has many interesting and important applications in such fields as communication networks, work assignments, scheduling, and coloring problems.  This presentation will show some ways that planar graphs can be used to explore coloring problems with origami polyhedral structures.
    In one simple example the planar graph of a cube can be used to explore various coloring schemes, using two, three, four, or more colors.  In a slightly more complex example a planar graph of a dodecahedron can be used to edge-color a 30 piece/3 color origami dodecahedron in such a way that each 3 different colors meet at each vertex.  Using a graph to explore coloring schemes gives the origamist an efficient tool to explore a wide variety of colorings.  Extensions to larger and more complicated origami polyhedra, where intuition about coloring is harder to exercise, will be discussed.
    In the mathematics classroom, students could construct an origami polyhedron. This could be used as a jumping off point for learning to draw planar graphs to explore various vertex, edge, or face coloring possibilities for various polyhedra. These could then be re-translated into origami objects.  Computer programs that include polyhedral graphs, such as the Poly Program, can be useful resources.
 

Investigating the Role of Axioms with Paperfolding
Jim Morrow (Mount Holyoke College)

Abstract: In a democratic society, it is critical to judge the claims of scientists, journalists, politicians, and advertisers. Validity and reliability of such information sources depend on the methods by which natural scientists, social scientists, historians, and others come to "know" things.  Axioms play an important role in the ways that we "know" mathematics, and the comparison to other fields of knowledge is illuminating.
    Traditionally, students have learned about axiomatic systems through high school geometry, college-level "foundations" courses, and other higher-level mathematics courses. This paper describes how paperfolding exercises for a first-year college geometry course can be used to illuminate and compare axiom systems for geometry and by analogy compare ways of knowing among disciplines and the undisciplined!
    We show how an axiomatic system can evolve from students methods of describing paperfolding moves to others. The variety of possible systems, including systems for other paperfolding geometries, Euclidean geometry, and non-Euclidean geometries, is illustrated. We will show how students have explored the characteristics of axiomatic systems and what makes a characteristic of an axiomatic system desirable or undesirable. Course web page materials are at  http://www.mtholyoke.edu/courses/jmorrow/info.html
 

In Praise of the Papercup: Mathematics and Origami at the University
Emma Frigerio  (University of Milan, Italy)

Abstract:  The traditional papercup was the starting point of a workshop held for students majoring in Primary Education at the Second University of Milan, Italy.  First, it is an easy model to teach people with no previous knowledge of origami and origami symbols.  Most importantly, it lends itself to many mathematical observations: a worksheet was designed to help students focus their attention on them (some formal proofs in Euclidean geometry were also requested).  Finally, some easy modules derived from it can be used to introduce modular origami.  A similar approach was used elsewhere in the workshop, whose main goal was to make students aware of the geometry underlying origami.  Other topics included: construction of modular regular polyhedra (and some stellations) fulfilling some assigned colour requirements, rectangles and similarity, an origami geometry theorem on triangles, approximate division of a sheet of paper in any number of equal parts.
 

Pi Basket
Kimberly Shuck (CA)

Abstract: In this talk we will explore a standard flat splint square to round basket and explore some of its mathematical implications.  Among these are the transition from flat materials to three-dimensional containers and a concrete way to consider the ratio that we call pi.
    Weaving with strips of paper produces a grid of square units that can be counted. This allows us to compare the various areas, perimeters and angles easily.
    Basketry has proven to be useful tool in the classroom because the materials are easy to come by, the technique is straightforward and the curriculum can be tailored to fit the needs of the students.
 

Teaching is Impossible!
Thoki Yenn (Denmark)

Abstract: Thoki will address the topic "Learning Origami" and writes that he will touch upon 1) the difference between teaching and learning, 2) the difficulties in learning in mixed groups, 3) the advantages of person to person instructions, 4) how to get a person in a mood of  willingness to learn, 5) adjusting the method according to the level of skill in the pupil, and 6) the importance of terminology.  However, Thoki has also sent us the following message:
     "Kalmon wants me to be sensible and serious, but I have to live up to the reputation and image
that I have worked so hard for, over the years: namely that this Thoki Yenn is crazy and moves
in mysterious ways around the borders of insanity, fighting the demons in his innner advisory council,
where Kalmon is the prime mover."
 
 
 

Science and Applications of Origami
 

Square Cycles: an Analysis of Flexagons
Ethan Berkove and Jeff Dumont (Lafayette College)

Abstract: In 1939 while a graduate student at Princeton, Arthur Stone invented what is known as a hexaflexagon, a hexagonal flat figure folded out of a strip of equilateral triangles.  This object can be flexed and rotated to bring different faces to view.  At the time of their invention, the flexagons were an interesting mathematical recreation.  They were also useful to topologists as an example of a Mobius strip, albeit an unusual one.  We intend to give a brief summary of hexaflexagons, their properties, and some classification information.  We will then turn to tetraflexagons, little-known relatives of the hexaflaxagon that are folded from squares.  The latter are barely discussed in the literature, and in many ways seem to be more interesting than their better-known cousins.
 

Exploring the Possibilities of a Module
Krystyna Burczyk, Wojciech Burczyk (Polish Origami Center, Poland)

Abstract: Rona Gurkewitz defined a modular system as a family of polyhedra models made from the same module. Usually the system contains only few models, because of constrains built-in into the module.  We concentrate on edge modules, i.e. modules which correspond to edges of a polyhedra. Modules of this type join in polyhedra to form vertices. There is no constraint on vertex degree, but the angle between two adjacent modules is bounded by some maximal value.  This constraint leads to maximal number of sides of each face.  An open frame 2 module by Tomoko Fuse is an example of edge module. Here the angle between two adjacent modules is limited by a right angle, so this module permits only triangle and square faces of open frame system models.  The construction of a dome allows us to go beyond this limitation. Two types of domes: small dome and large dome will be described. Domes give pentagon, hexagon, octagon and decagon polygons, which are required to build all of the regular (Platonic and Archimedian) polyhedra.  The mixture of small and large domes and different rotations of domes give additional effects.  Examples of the application of this technique to build polyhedra models are presented.
 

A Folded Deep Pot
Tomoko Fuse, Hiroshi Okumura (Japan)

Abstract: Folded deep pots can be made from a single sheet of paper.  Unlike other paper pots that consist of several pieces of paper held together with adhesives, these pots are made from a single piece of paper and no adhesive is necessary.  They can serve as paper containers for a variety of uses.  The design of these pots is based upon mathematical and engineering principles, and they can be made on a production line.
 

Multimodular Origami Polyhedra and their Duals, Made From a Family of Vertex Modules
Rona Gurkewitz (Western Connecticut State University), Bennett Arnstein (Los Angeles, CA)

Abstract: Modular origami polyhedra are generally made from a number of identical modules. In this paper we describe new polyhedra that are made up of more than one type of module from a family or system of modules.The family consists of the one-piece triangle, square, pentagon, hexagon and octagon modules by Simon, Arnstein and Gurkewitz. The one-piece triangle and square modules are one-piece analogues of the two-piece triangular and square gyroscope modules by Lewis Simon.
     The key to the construction of these polyhedra is the variation in size of the different modules which allows say a triangle module to fit together with a square module. We have constructed polyhedra based on the Archimedians and their duals, the Catalans, from these modules. We say "based on" because these new polyhedra are faceted beyond the basic polyhedra.
 

Airbag Folding: Origami Design applied to an Engineering Problem
Rainer Hoffmann (EASi Engineering GmbH, Germany)

Abstract: Today modern automobiles all have multiple airbags installed. Airbags are complex engineering systems with a folded textile structure as its core component. During the development of airbag systems, numerical simulation models are used extensively. The mathematical methods used, allow both the folding and forced unfolding of the airbag model. The paper demonstrates how folded airbag models are created and how their unfolding is simulated. It also shows how origami design techniques have been used to create simulation models for complex 3D-airbags.
 

Use of Origami in Fielding Very Large Space Telescopes
Roderick Hyde, Shamasundar Dixit (Lawrence Livermore National Laboratory)

Abstract: Very large, 25-50 meter aperture, space-based telescopes are crucial for advanced tasks such as the direct detection and observation of Earth-like planets around other stars. Fielding such large telescopes in space is particularly challenging because the telescope must be extremely lightweight, must be tightly stowed during launch, and yet deploy into a high-precision optical instrument.
    We are investigating a new type of space telescope, based upon Fresnel lenses rather than mirrors, which will enable very large apertures. These Fresnel lenses are flat, membrane-like, structures made from thin, lightweight, sheets of glass or plastic, which require 100,000-fold looser surface-shape tolerances (millimeters rather than hundreds of angstroms) than reflectors.
    One of the challenges to actually fielding such large membrane optics is stowing them for launch within a, relatively small, booster. Because the materials are delicate (glass breaks and plastic creases) this stowage must be done via careful folding rather than haphazard stuffing. Origami offers a method to efficiently package optical membranes; advantageous folding geometries permit flat segments joined at known fold-lines, fold into compact volumes, and deploy in a simple, controllable sequence.
    We are currently engaged in a project to build and demonstrate a lightweight, 5 meter diameter (Palomar-sized), foldable Fresnel lens. This is being constructed from an assemblage of 400 mm thick glass microsheets, each of which is optically patterned to form a segment of the overall Fresnel lens. The individual lens segments will then be precisely aligned and joined together (with foldable seams) into an origami pattern designed for this application by Robert Lang.
 

Polypolyhedra in Origami
Robert J. Lang (Specrta Diode Labs, Inc., CA)

Abstract: Modular origami -- origami constructed from many identical units -- finds its fullest expression in the representation of various mathematical families of polyhedra.  One of the more interesting families is the family of interlocking polyhedra typified by the Five Intersecting Tetrahedra that is the logo of this conference.  I call such interlocking polyhedra "polypolyhedra."  In this paper I will present a formal definition of a polypolyhedron and will present a systematic analysis of the uniform-edge polypolyhedra leading to a complete enumeration of same.  I will also present examples of their implementation with simple origami units.
 

On the Validity of the Orb and Other Origami Models
Jeannine Mosely (Belmont, MA)

Abstract: The folding and construction sequence of an origami model, together with certain assumptions about the properties of mathematically ideal paper, imply a system of constraints that defines the geometry of the model.  If the system of constraints has a solution, we call the model "valid".  We give examples of valid and invalid models, along with their constraint systems.  In particular, we analyze a questionable model known as "The Orb" and find it to be valid.
 

Organizing Global Shape through Local Interactions using Origami
Radhika Nagpal (Artificial Intelligence Lab, MIT)

Abstract: Amorphous computing is a project to build and understand systems that organize themselves to achieve predetermined goals, using only local computation and local communication. The dual goal is to learn how to engineer self-organizing systems as well as understand such phenomena in nature. In this talk I will present a language for describing the folding of a sheet of identically-programmed deformable cells to make predetermined global shapes, and a means of compiling that language into instructions for the cells. The global language is based on Huzita's axioms and the local instructions are inspired by mechanisms from developmental biology. I will show how the properties of Origami shed light on the creation of pattern and form in biology.
 

Circular Origami: a Survey of Recent Results
Eva Knoll, Ralph Baenziger (Architekten, Switzerland)

The geometry of paper folding finds particularly successful application through the use of circles. Though hardly traditional, the use of circular paper for Origami has produced, directly or indirectly, some interesting results. This paper proposes a survey of these results which we have obtained in the fields of Fine Arts, Education and Mathematics. In particular, some of the spin offs of the research include "Project Geraldine", the construction of a 10 foot Endo-pentakis-icosi-dodecahedron [1]. The author and her partner have also had the opportunity to use circular Origami to teach geometry to middle and high school children [2,3] as well as to explore classes of deltahedra with results carrying over into number theory [4]. These projects are the result of the first year and a half of systematic research into circular Origami, the chronology of which is the purpose of this paper.

[1]Bridges 1999: Barn-raising an Endo-pentakis-icosi-dodecahedron
[2]Bridges 2000: From the circle to the Icosahedron
[3]Bridges 2000: Polyhedra, learning by building: design and use of a math. ed. tool.
[4]ISAMA 2000: Decomposing Deltahedra

Bridges can be found at  http://www.sckans.edu/~bridges/  and ISAMA at  http://www.math.albany.edu/isama/2000/
 

Folded Tubes as Compared to "Kikko" ("Tortoise-shell") Bamboo
Biruta Kresling (Bionics and experimental design, Paris)

Developable surfaces with three pairs of scored sinusoidal lines are folded in extremely light and stiff tubular structures. This research started from workshops with French students in industrial design and bionics. The structures can be compared to abnormally grown "kikko" ("tortoise-shell" pattern) bamboo of particular mophologies and mechanics. This bamboo is highly appreciated for its strength and stiffness in Japan and shows an interesting mechanical feedback between growth and form. The bamboo could give some indications for design optimization of the folded tubes. Computer simulations of both structures are currently under research.
 

Origami with Trigonometric Functions
Miyuki Kawamura (Brookline, MA)

Abstract: When we create some origami works, especially geometrical ones, trigonometric functions (sin,cos and tan) are very useful tool for us. These functions connect length with angle.  Length is easy to handle via paperfolding because we know various origamic ways to divide an edge of paper.  On the other hand, almost all angles are hard to handle except for specific ones, for example 90,60,30 and 45 degrees.  At the 2nd. International Meeting of Origami Science and Scientific Origami, I presented a systematic way to construct arbitrary angles using trigonometric functions[1].  This method was as follows; first we provide a value of the trigonometric function for a certain angle.  Next we approximate this value to an appropriate fraction.  Finally, we can get this angle on a paper by folding.  Moreover, we can use trigonometric functions to solve an equation or an inequality, which gives some conditions for forms of origami works (or usually modules/units for me).  Here we make use of the property that trigonometric functions exchange an angle value to a ratio of two lengths.  Trigonometric functions and origami are very good friends, I believe.  These functions will make our origami life rich.  I hope that trigonometric functions become a standard tool for origami people.

[1] Miyuki Kawamura, "Polyhedron Origami:A Possible Formulation by 'Simple Units'",  Proceedings of The 2nd International Meeting of Origami Science and Scientific Origami in Otsu, Japan, 1995.
 

The Application of Origami Science to Map and Atlas Designs
Koryo Miura (University of Tokyo, Japan), Takahiko Kitsui (ORUPA CO., Japan)

Abstract: This paper reports applications of origami science to map and atlas designs. In terms of technical words, this is the problem of packaging 2-dimensional information printed on a sheet of paper into a smaller envelope.
    One of the subjects is the mass production of the so-called Miura-ori map. Since the innovation of the Miura-ori map in 1977, a few attempts to fold it by machine have met with small success. It seems that characteristic and useful properties of the Miura-ori are also the causes of that difficulty. Recently, a new method has been developed and the map publication using this method has started. Resultant sample maps will be shown at the symposium.
    The second subject is a new approach to atlas designs. The annoying property of conventional atlas designs is a break of continuity of 2-dimensional information at the page borders. In most of the published atlases a continuity is kept in the lateral direction, or west-to-east, but not in the vertical, north-to-south direction. On the basis of origami science, a new design that can keep the continuity in both directions is presented.
 

A Study of Twist Boxes
Noriko Nagata (Japan)

Abstract: Two types of twist boxes are presented; each of which is folded from a square sheet of paper and is surrounded on every side with four equivalent parallelograms.  Each parallelogram in the Type B-5 is folded mountain-like along a shorter diagonal and that in the Type B-6 is folded valley-like along a longer diagonal as shown in Figs.(a) and (b).  The properties of the twist of these boxes are characterized by the shape of the parallelograms, which are determined by the box's height and the positions of four corners of the bottom of the box on the square sheet. Here the structures of the two types of twist boxes will be analyzed mathematically and the results will be reported.

Scurls and Whirl Spools 
Chris K. Palmer (MD)

Abstract: Sets of Laves tiles with all combinations of C and S curves that allow spiral arrangements, studies of their properties and expressions of them as crease patterns on the plane will be presented.
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

The Foldin'ator Modeler and Document Generator
John Szinger (Zing Man Productions, NY)

Abstract: Sheet materials such as paper are ubiquitous in our society, and form the basis of numerous manufactured products.  However, artisans working in the domain of  folding and shaping sheet materials have been hampered by lack of availability of visualization and modeling tools common to other areas of design and production, working instead in the actual materials with all their cumbersome, incumbent overhead, and having no easy means of documenting their work.
     The Foldin'ator is an application for visualizing objects made by the sequential folding (and cutting) of flat sheet materials, and for generating annotated documents that record and  display the sequence of steps in the object's creation, providing a useful set of instructions to others.
     Such sequences can be used to represent origami models, packaging items, displays, and many other products.  In contrast to a generic 2D drawing or 3D CAD program, The Foldin'ator models the special qualities of sheet material, particularly its geometric configuration with respect to the constraints of manipulating 2D materials in 3D space, and also its thickness, flexibility and other properties. The Foldin'ator contains an object model for the sheet material and its geometric state, eliminating tedious redundancy on the part of the author trying to express such an object without the benefit of such a model, and allowing him to conduct simulations of the object under continual deformation.
 

"Is what you see what you think it is?" Unexpected Properties of the Square Frame in Origami Puzzle Design
Frances Winters (University of New England Armidale NSW, Australia)

Abstract: An interactive presentation of two new and challenging origami puzzles will be presented.  This provides an exploration of the way visual perception can both assist and inhibit thinking. The solutions show relationships with general Cantor Sets and Chladni figures.