
(1) Take a square piece of paper,
white side up, and accordion
pleat it into fourths.

(2) Fold the top left corner down.
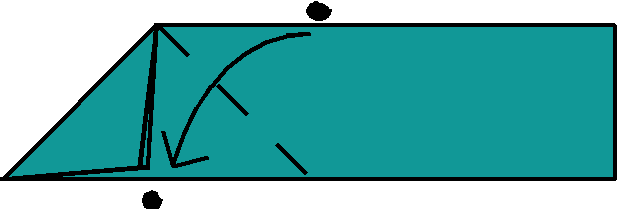
(3) Fold the right end of the strip
down to meet the folded edges.
|
Over the past several years I've been playing with a
certain member of the Zig-Zag family of
modular origami units. Zig-Zag units are
modular origami folds whose locking mechanism
is based on an accordion pleat. That is, you accordion
pleat a square, typically into 4ths or 3rds, making a
rectangle. The short ends of the rectangle become the
flaps, and the layers at the sides created by the accordion
folds become the pockets. Of course, other folds in the
rectangle are needed to make the flaps hook and stay,
but that's the basic concept. Lots of modular origami units
exist that fall into this category, units by creators such
as Robert Neale, Lewis Simon, Jeannine Mosely, and
Jun Maekawa, just to name a few.
The unit I've been using extensively is what I call the pentagon-hexagon zig-zag unit (or PHiZZ unit). I call it this because you can use it to make any polyhedron that
The unit itself is very simple, and the first thing I made with it was a dodecahedron. But then I noticed that the locking mechanism in this unit is particularly strong, allowing one to make much larger structures. Thus began my quest to see exactly what other polyhedra you could make with this unit and, later on, how to properly 3-color them. But first let's see how to fold and lock the PHiZZ units together. |
 (1) Take a square piece of paper, white side up, and accordion pleat it into fourths. |
 (2) Fold the top left corner down. |
 (3) Fold the right end of the strip down to meet the folded edges. |
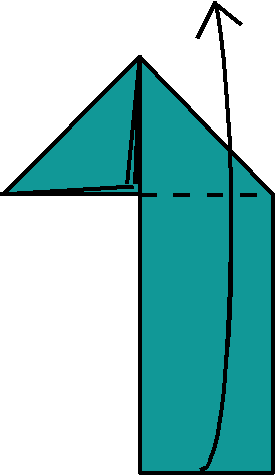 (4) Now fold the strip up, making the bottom flush. |
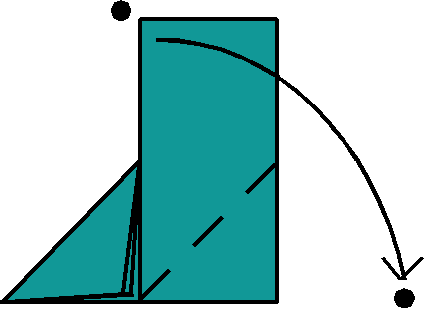 (5) Fold the strip down to the right. |

(6) Mountain-fold the upper right corner behind, and you're done with one unit! |
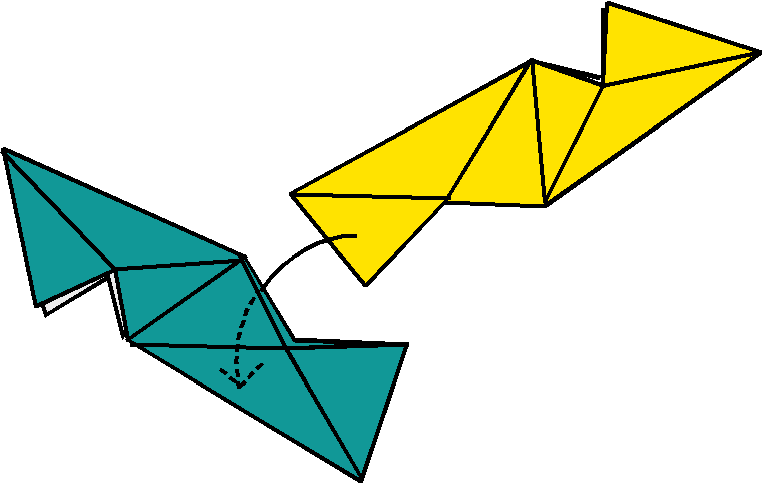 (1) Slide the end of one unit into the side of another, as shown. The flap should go in between the layers of paper, and crease lines should line up. |
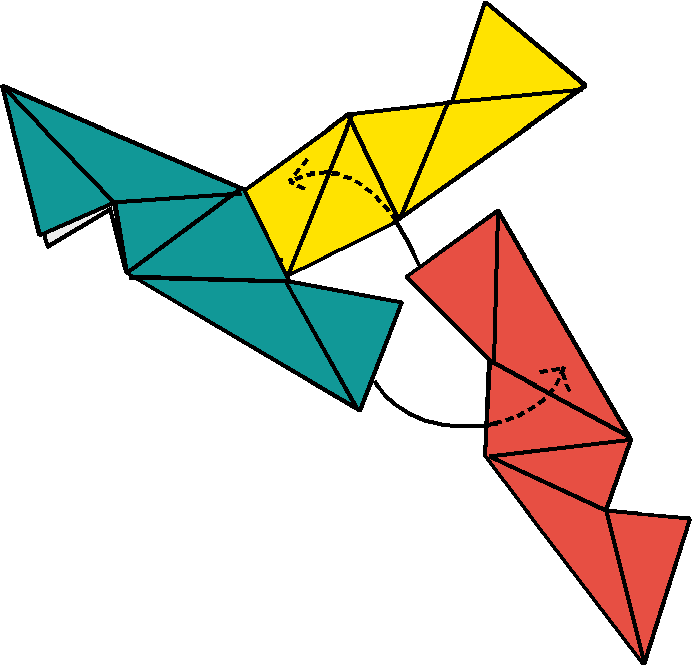 (2) It takes three units to make a "corner" of the polyhedron. Slide the third unit into the second unit, and slide the first into the third. |
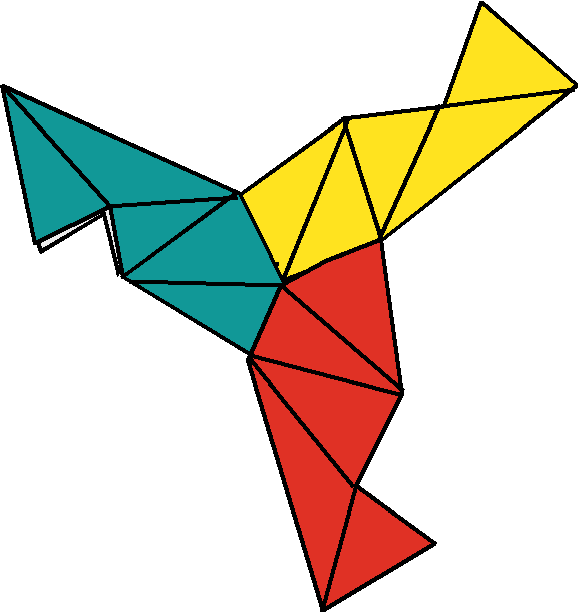 (3) This is what you should see. Notice how exactly half of each unit was used to make this "pyramid." Continue adding units to this to make your polyhedron. |
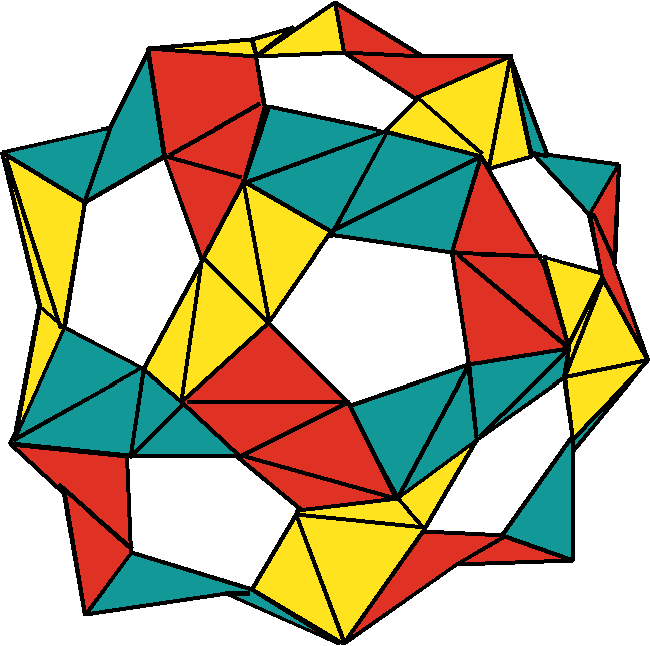
Adding units to your first three will begin to make a polyhedron, where each unit represents an edge of the polyhedron. Thus, the polyhedra made from this unit will look like polyhedral "frames" where only the edges are visible. The above object is a dodecahedron made from 30 pentagon-hexagon Z-units. It is the smallest structure that can be made from this unit. To make it, keep adding units onto your first three, but when you see five units going around a face, link them up to complete the face. This will make each face a pentagon, and will give you a dodecahedron. There are many different structures that can be made from this unit. In the next few weeks (or months??) I hope to add more to these pages about how to make bigger things and how many units it takes. I also have been exploring different ways you can color them. Until I write more about these subjects, think about the following exercises: (1) Make a soccer ball, aka truncated icosahedron, aka Buckminster fullerene, aka C60 molecule from this unit. It requires 90 units. (2) If 90 units is too scary for you, use 36 units to make a polyhedron with 12 pentagon faces and 2 hexagon faces. Is this polyhedron regular? (3) Make these objects using only three different colors, so that no two units of the same color touch. This is called a proper 3-edge coloring of the polyhedron. Figuring out where to put the colors is a puzzle, but not too hard, for the dodecahedron and the object in (2). But for the soccer ball it is quite a challenge! Click HERE for more info on making large Buckyballs! |