Rigidly-foldable Tetrahedron with a Slit
This web page describes joint work with Zach Abel, Robert Connelly, Erik Demaine, Martin Demaine, Anna Lubiw, Tomohiro Tachi, and myself. It is described in more detail in the paper "Rigid flattening of polyhedra with slits" which should be published in the 6OSME Origami^6 proceedings. (I'll post a link and publication data when it's made available.)
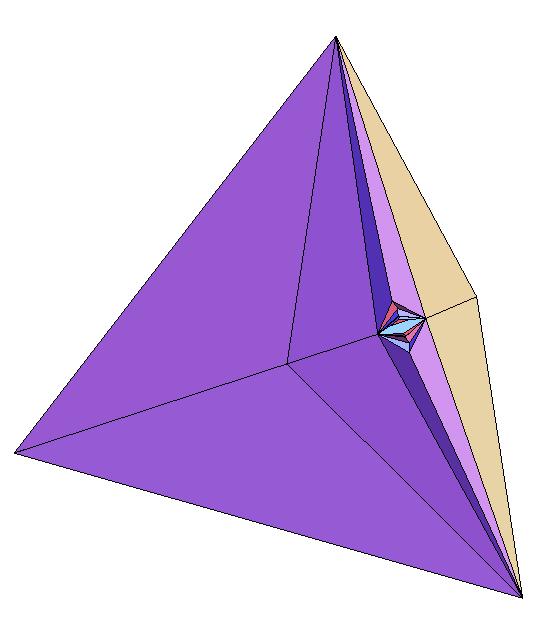
The bellows theorem states that a polyhedron cannot be rigidly folded or flexed in any way that decreases its volume. This means, for example, that if you have a regular tetrahedron then you cannot add creases to the faces to rigidly fold it, in other words collapse it into a flat state. But what if you cut the tetrahedron somewhere? Our group tried a variety of different places to put a slit into a regular tetrahedron, and we found that if we put a small slit perpendicular to and at the midpoint of one of the edges, then we could collapse the tetrahedron rigidly so long as we put an intricate network of creases around the slit on the tetrahedron face. We were able to make this slit very small as well; we can get it to a length of about 0.0461201 (where the length of an edge of the tetrahedron is 1).
Below are two animations from a symbolic Mathematica model that I made of our solution. The speed of these QuickTime movies is kind of fast, so please use the movie time controls to see the details. Both of the films show the folding tetrahedron with the minimum slit length 0.0461201. The movie on the right is a close-up of the slit during the folding process.