MA 323A Combinatorial Geometry!
Notes on Spherical Buckyballs -- Part 1
As mentioned in the instructions for making the PHiZZ unit, this unit can make polyhedra with only pentagon and hexagon faces. Such faces are made using "rings" of PHiZZ units locked together, as shown below.
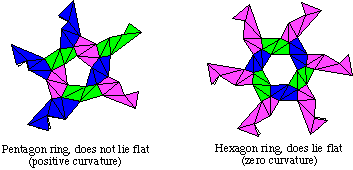
Before we go too much further, let's define Buckyballs formally.
Definition: A Buckyball is a polyhedron with two properties:
(1) every face is either a pentagon or a hexagon and
(2) each vertex has degree 3.
Exercise: Use Euler's Formula to prove that every Buckyball must have exactly 12 pentagon faces. (We did this in class.)
That exercise is very surprising! It says that no matter how big a Buckyball we make, we MUST have 12 pentagons, no more, no less. However, we apparently can have as many hexagons as we like. (Or can we?)
Definition: A Buckyball is called a spherical Buckyball if its 12 pentagon faces are evenly-spaced on the surface of the Buckyball.
That definition might not seem very rigorous, but it'll do for now.
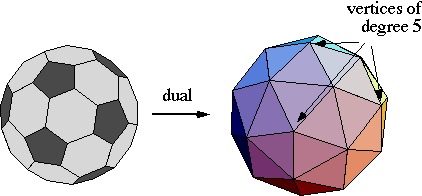
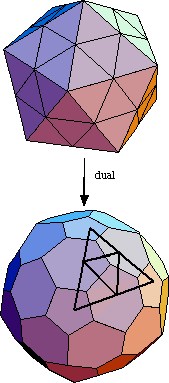
If we take the dual of a Buckyball, we get a geodesic sphere. Since a Buckyball has only pentagon and hexagon faces, it's geodesic sphere dual will have only vertices of degree 5 and 6. And since a Buckyball has only vertices of degree three, it's dual will have only triangle faces. For example, below is shown the soccer ball (truncated icosahedron) and its dual.

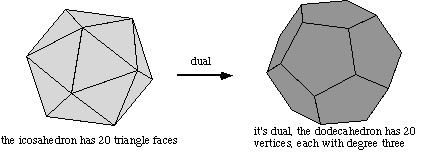
Making bigger Buckyballs: If we wanted to design spherical Buckyballs other than the soccer ball, we'd have to put more hexagons in between the pentagons. But how would we go about doing this? There are many ways to think about it, and all of them use the fact that the dual of the dodecahedron is the icosahedron.
Here is what we'll do: take each triangle face of the icosahedron and subdivide it into four smaller triangles, like so...

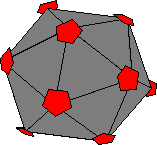
 To the right is shown what the icosahedron looks like when we subdivide each of
its faces in this way. Now, this creates new vertices, but notice that all the
vertices have either degree 5 or degree 6. This means that
the dual, shown to the lower right, will
have only pentagon and hexagon faces.
To the right is shown what the icosahedron looks like when we subdivide each of
its faces in this way. Now, this creates new vertices, but notice that all the
vertices have either degree 5 or degree 6. This means that
the dual, shown to the lower right, will
have only pentagon and hexagon faces.Furthermore, the only vertices of degree 5 in the subdivided icosahedron are the original corners of the icosahedron, before we subdivided it. This means that the pentagons in the dual will be "spread out" evenly, because the corners of the icosahedron are evenly spread out. Thus we do indeed get a spherical Buckyball when we do all this. (Note: this is not the soccer ball! We'll get to that later.)
Also, this construction gives us an easy way to understand the structure of the Buckyball. Each triangle side of the icosahedron was subdivided, giving us a "piece", or tile of what the whole subdivided icosahedron looks like. The dual of this piece gives us a tile of what this Buckyball looks like, shown below.
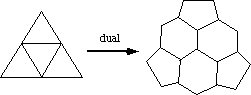
These tiles are of great help when trying to construct such Buckyballs using PHiZZ units. You don't have to keep the whole polyhedron in your mind at once. Rather, you can start by making one triangluar "tile" and then adding another "tile" to that, and another, and another, keeping in mind that each "tile" corresponds to a triangle face of the icosahedron. The only polyhedral structures that you have to keep in your mind are the icosahedron and one of these tiles!
Try it. This Buckyball has 120 edges, which means that you'll need 120 units to make it. Later, we'll use these tiles as a tool for coloring the units properly with only three colors, but even when made using all one color this object is quite stunning!
Larger and larger Buckyballs can be made using this subdivision method. But first let's introduce some notation that is used by people who study geodesic domes:
Definition: An n-frequency geodesic sphere is a geodesic sphere made by dividing each edge of the icosahedron into n equal parts and using this to subdivide each triangle face into smaller triangles.
For example, the geodesic sphere shown above was a 2-frequency sphere. Below is the tile for a 3-frequency sphere. It's dual gives a bigger Buckyball.
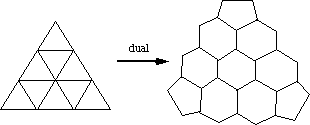

But also notice how in each of these tiles the pentagons are "pointing-in". That is, they're rotated so that one corner points in towards the center of the tile. For this reason, I like to refer to this family of Buckyballs as the pentagons pointing-in, or PPI family of spherical Buckyballs. Any n=frequency geodesic sphere will give us such a PPI Buckyball when we take the dual.
But these are not the only Buckyballs we can make! The saga of all this continues in Part 2 of these Buckyball notes!
Return to Combinatorial Geometry Page