(Jun Maekawa's Devil, folded from one square of paper, no cutting)
Midterm Paper Project
Assignments:
PS 1: Due Feb 3
PS 2: Due Feb 10
PS 3: Due Feb 17
PS 4: Due Feb 24
PS 5: Due March 3
PS 6: Due March 31
PS 7: Due April 12
PS 8: Due April 21
PS 9: Due April 28
Oh look! It's
The Final Exam!!!
Due on the final day, May 11
Here are some handouts:
(all are in PDF format)
Capped Octahedron Bomb
PHiZZ Unit
Business Card Unit
Bigger PHiZZ Unit Rings
BOO 6 Activity
Coloring a Crane
MA 323A Combinatorial Geometry!
Notes on Planar Graph Theory
Notes on how to do Proofs!
Notes on Buckyballs (Part 1)
Hi! This is the web page for the Spring 2005 course Combinatorial Geometry at Merrimack College. Make sure to check this web page regularly for class notes and updates.
Combinatorics (the mathematics of counting) and geometry have many strong connections. We will explore these connections by looking at 3D polyhedral geometry and the mathematics of paperfolding (origami). In particular, we'll cover...
Convex Polyhedral Geometry: construction of paper models, Euler's Formula,
planar duality, coloring theorems, Hamilton cycles, Buckyball classification
and edge coloring, spherical geometry, solid angles, Descartes' Theorem,
surfaces of higher genus, convex polytopes, simplices, the Generalized Euler's
Formula.
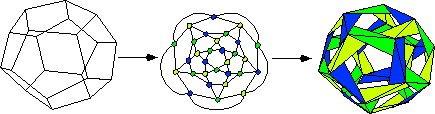
Axiomatic and Analytic Modelling of Paper Folding: The classic straight-edge and compass axioms, origami axioms, analytic paper folding, constructing divisions of the square, trisecting angles, envelopes of curves, solving cubic equations, Haga's Theorem.
Combinatorial Modelling of Paper Folding: Maekawa's Theorem, Kawasaki's Theorem, local and global conditions for flat-foldability, NP-completeness, counting foldings, 3D solid paper folding, twists and origami tessellations, the Rabbit-Ear Theorem and origami design, isometries of the plane, high-dimensional flat folding.
There are no math books out there (yet!) that cover this material, so there will be no text for the course. This means that you all will have to take very good notes! To help, I will try to put important definitions, pictures, notes, and things on this web page, so be sure to visit frequently!