Five Intersecting Tetrahedra

About the object

This visually stunning object should be a familiar sight to those who frequent the landscapes of M.C. Escher or like to thumb through geometry textbooks. To construct an origami version it is essential to have a good understanding of the object's structure, which the accompanying pictures try to illustrate.

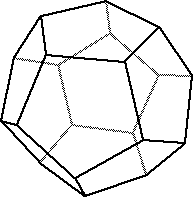
To the right is shown a dodecahedron - the classic polyhedra with 12 equal sides. If we were to take 4 equidistant corners of the dodecahedron and connect them with lines, the result would be a pyramid (a tetrahedron) inscribed in the dodecahedron. This is illustrated below.

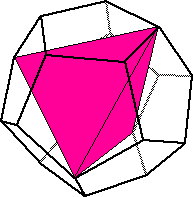
This tetrahedron has 4 corners, and the dodecahedron has 20 corners total. Thus we could inscribe 5 distinct tetrahedra inside a dodecahedron! The result of doing this is shown below.

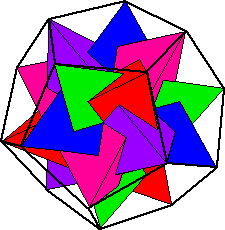
Thus the left hand picture illustrates what five intersecting tetrahedra look like, and notice how all these pyramids are cutting into each other. Suppose we replaced these pyramids with tetrahedral frames. Provided we made the frames thin enough, they wouldn't cut into each other anymore, and the result (shown to the right) would be an intricate woven nest of 5 tetrahedra. This is what we shall construct via modular origami!

So here is the task: Given this wildly complex-looking structure, how do we make it out of modular origami units? Well, if we could make a modular tetrahedral frame we'd be 90% there, right? I mean, in theory at least, if we could make a tetrahedral frame of sufficient thinness then all we'd have to do is make 5 of them and figure out how to weave them together. Yes, that last part (the "weaving") is the hardest step, but before we can even think about that we need to find a tetrahedral frame unit.

And what do ya know? A good perusal of the origami literature reveals a perfect unit for our task! In the December 1986 issue of the British Origami Society Magazine (No. 121, p. 32) we see Francis Ow's "60 degree Unit". This unit is made from a 1x2 piece of paper and produces a frame that's too thick for our purposes. That is, the width of the frame is too thick to allow 5 tetrahedra to be woven together as per the previous page. But if we instead fold Francis Ow's unit from a 1x3 piece of paper we'll be in buisness!

Francis Ow's 60 degree Unit

Making one tetrahedron frame requires six 1x3 pieces of paper. In other words, it will take two squares which then must be cut into 1x3 strips. To make the full 5 intersecting tetrahedra model you'll need to make 5 of these tetrahedra - that's a total of 10 squares of paper. To make each tetrahedron a different color, as in the picture above, you'll thus need 5 different colors and 2 square sheets per color.

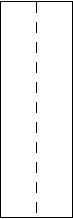
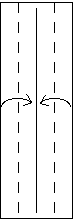
Take one of the 1x3 strips (white side up) and crease it down the middle. Then fold the sides to the center line. The right-most picture shows a close-up of the top end. Fold the right flap to the side, only making a pinch! This crease will be needed for the next step.

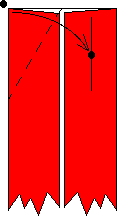
Then fold the upper-left corner to this crease line, making sure that the crease hits the midpoint of the top edge, as shown in the left-most picture. (Note that this is axiom (O5) in Huzita's axiom list (see Origami Geometric Constructions), and creates a 60 degree angle for us!) Then fold the upper-right corner over this flap, and unfold these flaps.

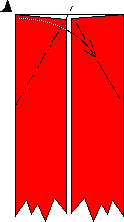
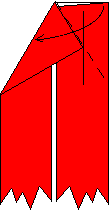
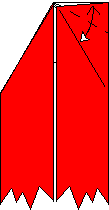
Now reverse fold the upper-left corner, using the crease that we just made. The reversed flap should go inside the model. Then (right-hand picture) fold and unfold the top edge of the right side to the existing crease line.

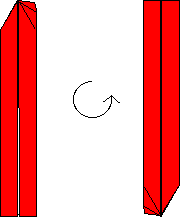
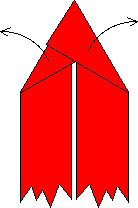
OK! We're done with one end, so rotate the model 180 degrees and repeat this process on the other end. (Note that the unit will have a left-handedness, like the Sonobe unit, and all of your units must have the same handedness in order to fit together properly.) Lastly, crease the unit down the middle, and you're done! You'll need 5 more to make one tetrahedron.

How to interlock the units

The end of each unit has a flap on one side and a pocket on the other. Insert the flap of one unit into the pocket of another as shown on the left. To the right is the result. Notice the nifty x-ray view effect, allowing you to see exactly how the flap needs to hook around the crease. This makes a strong lock.

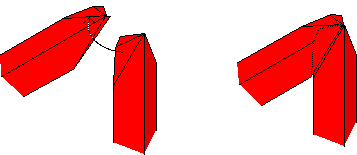
Now get ready to insert the third unit! This should complete one "joint" of the tetrahedron frame. Notice that each unit should form a "wedge" (in cross-section). However, when insertig the last one you might want to round-out the edges, so as to allow the last flap to hook around the other unit. Then pinch the sides to make everything stay in place.
To build on this tripod you've just made, add two units to one of the tripod's legs to make another "joint". Then the last unit can be added to complete the tetrahedron.

Forming the object

Unfortunately there's no easy way to describe how the tetrahedral frames need to weave around each other to create the 5 intersecting tetrahedra model. It really is a challenging puzzle to put it all together! I suggest that you use the following series of pictures to guide you in weaving one tetrahedron at a time.

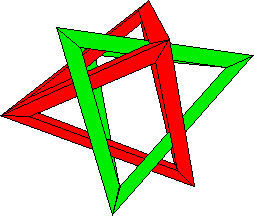Notice how, in the right-hand picture, the left-most corner of the red tetrahedron is poking through a "hole" of the green one, and vice-versa, the right-most corner of the green tetrahedron is poking throught a "hole" of the red one. Further, this is done symmetrically. This observation is key to understanding how the tetrahedra fit together. Inspect the next pictures very carefully!

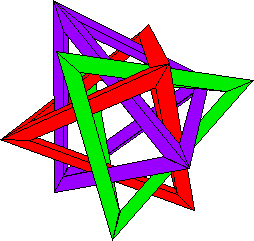
There is a very strong symmetry behind the formation of this structure, and understanding this symmetry can aid you in the construction. The finished object should have the following property: any two tetrahedra are interwoven with one corner poking through a hole of the other and vice versa, kind of like a 3-D Star of David but slightly twisted. (This is what we tried to describe above.)

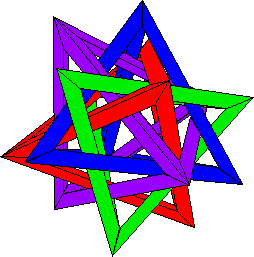
The important part, though, is that every pair of tetrahedral frames in the finished model should have this property. I admit that this is a hard concept to grasp, but it can help in checking to see if you're "weaving" the frames properly.

Again, completing this model is a challenging puzzle, and the difficulty of this challenge is reflected in the fact that the finished model is nothing less than stunning. People's first reaction, when being shown the object, is usually to stop and stare at it for a few hours in fascination. Try it!

Exercises:

(1) Francis Ow uses his "60 degree Unit" to make frames of other polyhedra as well. What other Platonic Solids can be made from this unit?

(2) Think about this "woven 5 tetrahedral frames" object for a moment. If the frames are too thick, the model is impossible to make. But if the frames are too thin, the tetrahedra will fall loose around each other and look like a mess! Between these extremes there's a certain frame width that is perfect, that is, will make the units fit snuggly together. When made from 1x3 pieces of paper, Francis Ow's unit makes frames that are 1/12th as thick as the edge of the tetrahedron. Is this the "perfect" width? Or is it just "close enough"?

(3) Think about the "5 intersecting tetrahedra" object that we looked at before turning the tetrahedra into tetrahedral frames (shown again on the right). Wouldn't it be cool to create a modular origami unit that produces this object? Try it!

Back to Origami Mathematics page