Origami and Geometric Constructions

a comparison between straight edge and compass constructions and origami

In high school geometry students examine the types of geometrical operations that can be performed by using only a straight edge and a compass (SE&C). One learns how to draw a line connecting two points, how to draw circles, how to bisect angles, how to draw perpendicular lines, etc. In fact, you may remember that all SE&C constructions are a sequecne of steps, each of which is one of the following (taken from What is Mathematics? by Courant and Robbins, Oxford Univ. Press, New York, 1941):

Given two points we can draw a line connecting them.
Given two (nonparallel) lines we can locate their point of intersection.
Given a point p and a length r we can draw a circle with radius r centered at the point p.
Given a circle we can locate its points of intersection with another circle or line.

This list of axioms encompasses everything you can do with a SE&C. That is, anything you do with a SE&C can be broken down into a sequence of the above operations. Using this axiom list, one can begin to talk about things that cannot be done using a SE&C. For example, students are traditionally told that certain things are impossible to do with a SE&C, like trisecting an arbitrary angle, or doubling the volume of a cube (i.e., constructing the cube root of 2). Hearing this usually makes students spend hours and hours trying to trisect an angle using SE&C (I know I did!), but alas, this really is impossible. Unfortunately, proving that it is impossible requires some high-level math, like abstract algebra, which is beyond the reach of most sane adults. However, we can also make geometric constructions with origami, using the side of the paper as the straight edge and folding up to an angle to simulate a compass. Furthermore, trisecting angles and doubling cubes is possible with origami! Seeing this can lead to a greater understanding of why these things are impossible with SE&C, and is the main topic of this web tutorial.

Huzita's Origami Axioms

Please note that paper folding can be quite complex! There are many intricate paper folding maneuvers, and harnessing the power of origami through a list of axioms, like we did above for SE&C, is tricky. ( Footnote 1) The Italian-Japanese mathematician Humiaki Huzita has formulated what is currently the most powerful known set of origami axioms (from his article, "Understanding Geometry through Origami Axioms" in the Proceedings of the First International Conference on Origami in Education and Therapy (COET91), J. Smith ed., British Origami Society, 1992, pp. 37-70):

(O1) Given two points p1 and p2 we can fold a line connecting them.
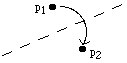
(O2) Given two points p1 and p2 we can fold p1 onto p2.
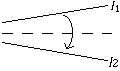
(O3) Given two lines l1 and l2 we can fold line l1 onto l2.
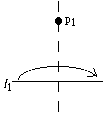
(O4) Given a point p1 and a line l1 we can make a fold perpendicular to l1 passing through the point p1.
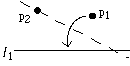
(O5) Given two points p1 and p2 and a line l1 we can make a fold that places p1 onto l1 and passes through the point p2.
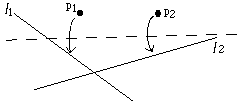
(O6) Given two points p1 and p2 and two lines l1 and l2 we can make a fold that places p1 onto line l1 and places p2 onto line l2.

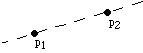
Huzita's axioms (O1)-(O4) are rather simple, and it's easy to see that they are operations that can also be done by a SE&C. (O5) and (O6), on the other hand, take some getting used to. First let's look at (O5), which can also be done using SE&C, but just what is this axiom doing?

Exercise for Axiom (O5)

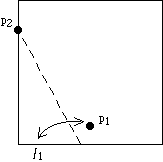
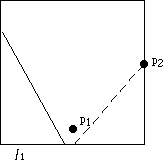
Take a square piece of paper. Let the bottom edge be l1 and take p1 to be a point in the middle and close to l1. Then choose p2 to be anywhere on the left or right edge of the square and perform axiom (O5). Then choose a different p2. Repeat this 8 or 9 times. What do you see?

Solution and moral of this exercise

Exercise for Axiom (O6)

Don't do this exercise until you've done the previous one! If you look closely, axiom (O6) is just like (O5) but times two: In (O5) p1 is the focus and l1 is the directrix of a parabola. In (O6) we have this again, but also p2 is the focus and l2 is the directrix of another parabola!

Thus axiom (O6) solves the following problem: Given two parabolas drawn in the plane, find a line that is tangent to both of them.

Exercise: Show that doing this is equivalent to solving a 3rd degree equation.

The solution is left to the reader, but note that it might require some algebraic geometry.

Moral of the exercise: Axiom (O6) can solve cubic equations. This is something that SE&C cannot do. Further, the problems of trisecting angles and doubling cubes all reduce to solving cubic equations. Thus axiom (O6) should allow us to solve these problems via origami. Indeed, it can!

How to Trisect an Angle via Folding

This method is by H. Abe (from "Trisection of angle by H. Abe" (in Japanese) by K. Fusimi, in Science of Origami, a supplement to Saiensu (the Japanese version of Scientific American), Oct. 1980, p. 8).

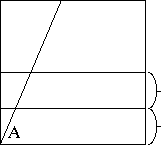(1) Let the angle you want to trisect originate from the lower left corner. Call this angle A. (Note that here we assume that A is acute, but this method is easily extendable to obtuse angles.) Make two parallel, equidistant horizontal creases at the bottom.

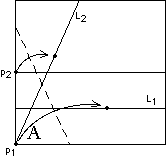(2) Then perform axiom (O6). Fold p1 onto L1 and p2 onto L2. This isn't easy to do! You may have to play with the paper in order to find the exact location for this fold.

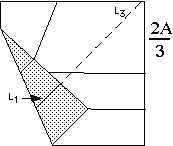(3) With this folded, refold crease L1, now in its new position, and extend it all the way up. This new crease, L3, is the crease we want. Unfold step 2 and extend crease L3 to the lower left corner (it should hit it!). The crease L3 will mark the angle (2/3)A.

Exercise: Can you prove that this method works? That is, can you prove that line L3 meets the lower left corner at an angle of (2/3)A?

Solution.

How to double a cube via folding

"Doubling a cube" means doubling the volume of a given cube. The real challenge for doing this is constructing a line with length equal to the cube root of 2. This is a solution of a cubic equation, and thus we need to be able to solve cubic equations to succeed. SE&C can't do it, but origami can.

Peter Messer has an amazingly elegant way to do this with paper folding. (From Problem 1054, in Crux Mathematicorum, Vol. 12, No. 10, 1986, pp. 284-285.)

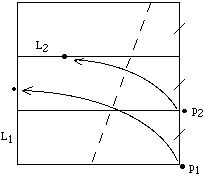
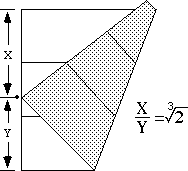
First fold a square into thirds. (There are mathematically accurate ways of doing this, but we'll skip that.) Let p1, p2 and L1, L2 be as shown, and perform axiom (O6). Denote lengths X and Y where the point p1 lands on line L1. Then the ratio X/Y is the desired number, the cube root of two.

The proof of this is left to the reader!

These are just a few examples of how axiom (O6) can be used to perform complicated constructions. There are many more, and readers encouraged to experiment and discover their own!

This tutorial is only an introduction to the subject of origami geometric constructions. For a more rigorous development, see the original articles by Humiaki Huzita and Robert Geretschlager (referenced in the origami geometry section of the Origami Math Bibliography). Although for a complete understanding of these concepts the reader should investigate any of the numerous writings on SE&C constructions, for example Chapter III in What is Mathematics? by Courant and Robbins (Oxford Univ. Press, New York, 1941) or Chapter 7.5 in A First Course in Abstract Algebra, Fifth Ed. by Fraleigh (Addison Wesley, Reading, 1994).

There is a more historical context in which we can view origami constructions. Although SE&C is not enough to trisect angles, one can trisect angles if we allow ourselves to use a ruled straight edge. In classic SE&C constructions the straight edge is used only to make a straight line, but mathematicians as far back as Archimedes (see Courant and Robbins, What is Mathematics?, p. 138) knew that if two marks were made on the straight edge (for measuring) then trisections could be performed. In this view it makes perfect sense that origami constructions allow things like trisections, since the straight edge of the paper could easily be "ruled" by pinching the 1/2, 1/4, 1/8, ... divisions along the side. Yet so far no detailed comparison between origami constructions and ruled SE&C constructions has been made.

Also, we do not know if Huzita's axiom list is complete! Might there exist some other folding operation that would allow us to solve equations of degree 5 or higher? The general consensus seems to be that no such "7th axiom" exists, but no one has proven this.

Update (5/16/03): The above tutorial needs to be updated and revised. I'm not sure when I'll have time to do it. However, a number of readers have noticed some inconsistencies in Huzita's axiom list. Such concerns stem from the need to set things up more rigorously, if we're to be more precise. For example, we usually fold our origami constructions starting with a square piece of paper (or a rectangle). Therefore, we should think of all our constructions as starting in the following way: Given: four points (say, p1=(0,0), p2=(1,0), p3=(1,1), and p4=(0,1) (which correspond to the four corners of our square paper) and the lines L1=p1p2, L2=p2p3, L3=p3p4, and L4=p4p1. Then we ask ourselves, "What are the basic origami operations we can perform on this starting set of points and lines?" When done formally, in this way, many of Huzita's axioms are redundant, and the list of necessary basic folding operations becomes MUCH smaller.

Also, several researchers have been making advances into the question of whether or not there are other "origami axioms" that are yet undiscovered. Erik Demaine, Robert Lang, and Koshiro Hatori (see his web page) have been doing exciting things in this area.

For a much more rigorous presentation of origami geometric constructions, see Roger Alperin's paper "A mathematical theory of origami constructions and numbers" which appeared in the New York Journal of Mathematics in 2000. It can be downloaded (in PDF and ps format) here.

Back to Origami Math pages