MAMT 574-52 Origami in Mathematics and Education

Welcome! If you're looking at this web page, then you're either registered for or planning/thinking of registering for the class MAMT 574-52 Origami in Mathematics and Education for the Winter 2022 term at Western New England University.

Here you will find some information about the course. More details will be provided in the course syllabus. Please feel free to EMAIL ME if you have any questions!

Interested in this course, but not an MAMT student? Then you can apply to enroll in the course as a non-degree student. WNE charges $1260 for our MAMT courses (which is fairly cheap as these things go). Here is the non-degree study application and here is the listing of 2022 Winter Term courses (scroll down till you find the Mathematics for Teachers section).

Online course: This course will be conducted online in a synchronous format. (Actually, all of our MAMT courses are being conducted online, synchronously, right now, and this will likely continue for some time.) Specifically, this means:

• Classes will be conducted over Zoom at our prescribed class times (see below, MW at 6:00pm-7:50pm Eastern Time Zone), with lectures given in real-time by me and group work conducted in Zoom breakout rooms.
• We will use the online, shared whiteboard platform Limnu for lectures and group work activities. Note: Using online whiteboards is much easier if you have a tablet (like an iPad) or a touch screen and a good stylus.
• Students will be required to keep their Zoom cameras on at all times as a way to create classroom community and model an in-person class as much as possible. (Students may choose to use a "background filter" in Zoom to keep their surroundings private.)
• We will also use WNE's course management platform, Kodiak, to handle course communications, uploading of homework assignments, exams, and grading.
• Since the class is about origami, there will be folding activities done during class time. Participants will need paper for this purpose. Students who are within driving distance to Western New England University (in Springfield, MA) may choose to visit the campus and be given suitable origami paper from the instructor, Tom Hull. Otherwise, students will have to get their own paper:
  • A pack of 3.5 in square Memo Cube paper from Staples (500 sheets).
  • A pack of 6-in origami paper that is colored on one side and white on the other. This can be also be found at Staples (but is kind of expensive there), or can be found at most art supply stores, like Michaels (notice, much cheaper!). But I recommend buying this origami paper from OrigamiUSA, the national, not-for-profit origami society.
  • You will also need some standard, rectangular paper for folding, like 8.5 x 11 in paper in the USA or A4 paper in other countries.

Textbooks: None, officially. However, some people really like to have a textbook to use as a reference. Much of what we do will follow things in the following books:

• Project Origami: Activities for Exploring Mathematics, 2nd edition by Thomas Hull, A K Peters, 2012.
• Origametry: Mathematical Methods in Paper Folding by Thomas Hull, Cambridge University Press, 2020.

Buying these books is OPTIONAL.
Let me elaborate. I feel uncomfortable requiring you all to buy books that I wrote (although I only get something like $5 for each book sold). And in theory you do not need to have these books. The activities we do in class will be self-contained, and I will be writing problem sets for homework (one per week) and posting them on Kodiak. BUT many people like to read things on their own, in addition to our class notes. If that describes you, then you might want to get one or both of these books. Project Origami is full of activities and worksheets to be used in classes to teach origami-math concepts (some of which we will use in our class). Origametry is more like a textbook and is written at a more advanced level than Project Origami. The paperback versions of both books are definitely cheaper than the hardcover versions (about $55 for Project Origami and $39 for Origametry). (And right now, Origametry is cheaper on Amazon, while Project Origami is cheaper on the publisher's web page, at the above link).

Meeting times: Mondays and Wednesdays from 6:00pm - 7:50pm (Eastern Time Zone), Jan. 19 - March 30, 2022.

Instructor: Tom Hull, Associate Professor of Mathematics, WNE. Office: Herman 308-G

Description: Origami, the art of paper folding, has strong connections with mathematics. The process of folding paper can be explored and modeled with geometry, algebra, number theory, combinatorics, graph theory, calculus, linear algebra, and many other branches of math. This makes origami a perfect medium by which math teachers of all levels can infuse hands-on, fun, paper folding explorations into their classes. In this course we will examine the many ways in which origami can be studied mathematically, giving us a chance to see how many different branches in math can come together around one subject. We will also pay special attention to how such origami projects can be used in middle-school and high-school math classes. This will be a very hands-on class, with many opportunities for participants to fold things for themselves and prove the math behind the folds. 3 cr. (CORE)

Topics covered: As the course description states, we will be using many different brances of math in this course. Since everyone has different backgrounds, this will require reviewing some basic material in-class. However, the subjects we will be making the most use of will be the following:

• Geometry (standard Euclidean geometry, like similar triangles, as well as analytic geometry, using equations of lines and parabolas and such)
• Graph Theory (studying 3D polyhedra as planar graphs is very useful, and we will pay particular attention to graph drawing, cycles on graphs, and graph colorings)
• Combinatorics (suprisingly, a lot can be learned about paper folding by doing things like counting the number of mountain creases and valley creases in a folded object's crease pattern, so combinatorics is a very good tool to use)
• Applications Origami is being used to deploy solar panels in outer space, to design better air bags for cars, and to even make heart stents. In fact, the instructor of this course (Tom) worked with some physicists at UMass-Amherst to apply origami to soft-matter polymers, with hopes of creating new biomedical devices (for example).
• Other stuff! (We will see some matrices. We will see some number theory. We might even use some calculus, complex numbers, or abstract algebra! All of these topics will be reviewed as they are introduced.)

Grading: Your grade for the class will be determined by the following:

• 30% Midterm exam
• 30% Final project and presentation
• 30% Homework
• 10% Participation

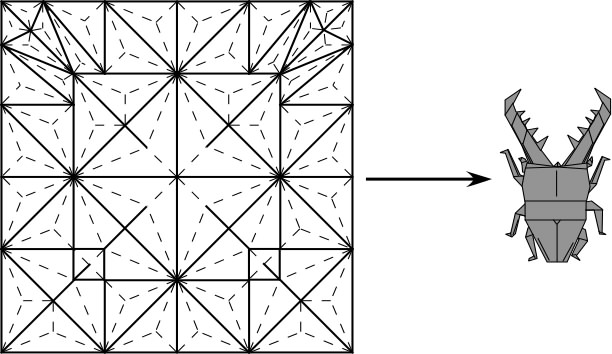
About Folding: There will be a fair amount of paper folding done in class and sometimes for homework. Please do NOT be worried about your own personal paper-folding skill. Most of what we will fold will be at the simple level (although they will use math!) and not complex bugs like the one shown above. However, we will study the math behind such complex-level origami. Those students who do wish to explore such advanced paper folding will have opportunities to do so.

About the instructor: Thomas Hull has been practicing origami since he was 8 years old. He has co-authored two origami instruction books (Origami, Plain and Simple with Robert Neale (1994), and Russian Origami with Sergei Afonkin (1997), both published by St. Martin's Press) and has invented numerous origami models. His PHiZZ Unit has been especially popular, and his Five Intersecting Tetrahedra model was voted by the British Origami Society as one of the top 10 origami models of all time. From 1994-2007 he was on the board of directors for OrigamiUSA, a national nonprofit organization for the advancement of origami. He is also one of the world experts on the mathematics of origami. He edited the book Origami³ (the Proceedings of the Third International Meeting of Origami in Science, Mathematics, and Education) and authored the optional texts for this course, Project Origami and Origametry. He has been invited to lecture on the mathematics of origami across the USA as well as in Peurto Rico, Europe, and Japan. In other words, this is his specialty and this will be an awesome class!

Links: There are a lot of great resources for origami, and origami-math, online. Below are a few links to explore (feel free to search for more) if you want to get a feel for what origami is all about.

• Robert Lang's web page, which contains pictures of fantastic models as well as information on origami applications in math and science.
• My origami math pages, which are some of the oldest origami-math pages on the web! There are instructions for some of my models as well as previews of some things we'll see in class.
• The web page of OrigamiUSA, which has all sorts of resources for matters origami.

Last updated: 12/4/2021

Return to Tom Hull's home page