Tom's Origami Research Corner

What is origami mathematics?

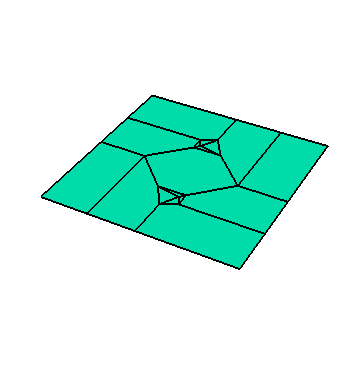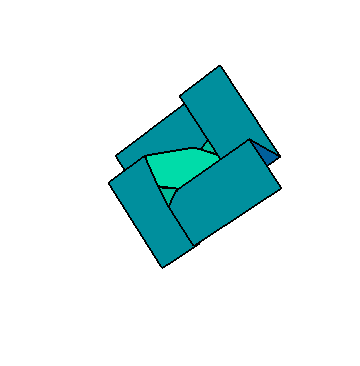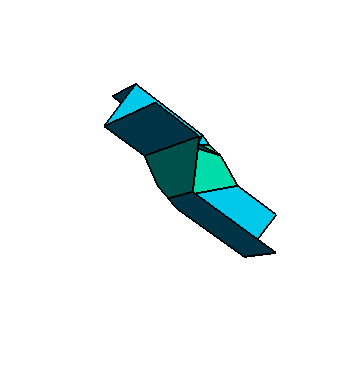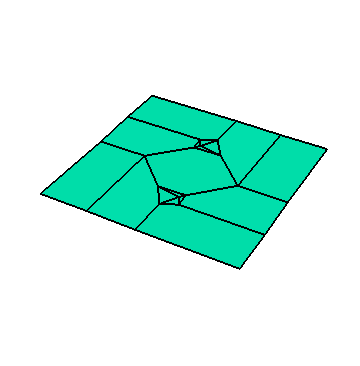
Origami is the art of folding paper. In the scientific research community, however, the word origami is being used to describe any kind of folding process. This could be strands of DNA folding inside a cell or in a lab (which can be modeled by 1-dimensional origami, like folding a string). Or it could be folding a flat solar panel array into a compact package that could be rocketed up into outer space (that would be 2-dimensional origami). Being able to design or control such folding mechanisms requires a deep understanding of how they work, and that's where the math comes in.

I am interested in all of the myriad ways in which mathematical methods can be used to understand folding processes, what I call origami mathematics. In this research I collaborate with many people. Some are mathematicians, while others are computer scientists interested in computational origami, engineers interested in folding mechanics, and physicics interested in origami applications in materials science.

On these pages you will find listings of current/past projects, collaborators, students, and funding sources for my research.

Want to know more?

My new book, Origametry: Mathematical Methods in Paper Folding has been published by Cambridge University Press!

This book offers an introduction to the mathematics of origami. It is organized into four parts:

• Geometric Constructions
  See how origami is more powerful than straightedge and compass constructions.
• The Combinatorial Geometry of Flat Origami
  Here the rich field of flat origami theory is developed, with attention to the combinatorial structures that it contains.
• Algebra, Analysis, and Topology in Origami
  This contains examples of how various aspects of paper folding can be best modeled using either algebra (origami homomorphisms that capture the symmetry group of crease patterns and their folded images), analysis (how polyhedral origami folds can offer solutions to certain partial differential equations), or topology (folding compact manifolds in arbitrary dimension).
• Non-flat Folding
  Three-dimensional, polyhedral origami is explored in this part, with particular attention to rigid origami, rigid folding motions, and configuration spaces.

---

Work supported by NSF grants DMS-2347000, RUI: Configuration Spaces of Flexible Polyhedral Surfaces, DMS-1906202, RUI: Configuration Spaces of Rigid Origami and EFRI-1240441 Mechanical Meta-Materials from Self-Folding Polymer Sheets.

Contact: Feel free to email me at thomas.hull and then "at" and then "fandm" dot "edu".

Or vist me at my professional web page or find me at Franklin & Marshall College.

Last updated 9/24/23