Tom's Origami Research Corner
Configuration spaces of rigid foldings
This long-term project concerns rigid origami, where we imagine that we are folding stiff (but mathematically thin) metal and have (mathematically thin) hinges at the creases. Will we be able to smoothly fold and unfold such origami? If we can, then tag each crease with a number pi = the folding angle, the amount that the crease bends from the unfolded state. If the crease pattern has n creases, then the set of all points (p1, p2, ..., pn) made by the folding angles gives us the configuration space of the rigidly-foldable crease pattern. Understanding the configuration space gives us valuable information for using rigid origami crease patterns in applications.
Publications:
- A rigid origami elliptic-hyperbolic vertex duality, Thomas C. Hull, Results in Mathematics, Vol. 80, Article 138, 13 pages (2025).
Supplementary video 1: SM1.m4v
Supplementary video 2: SM2.m4v
-
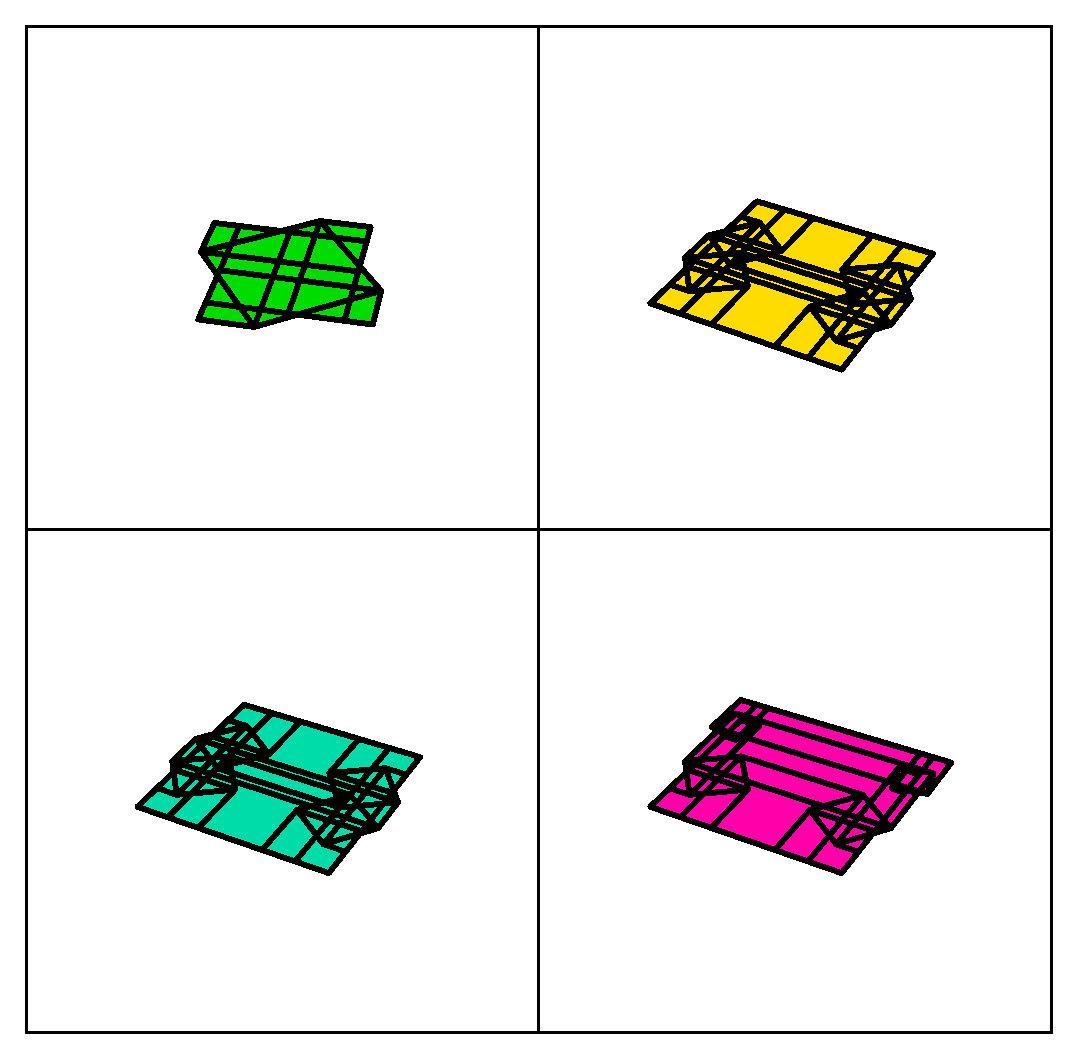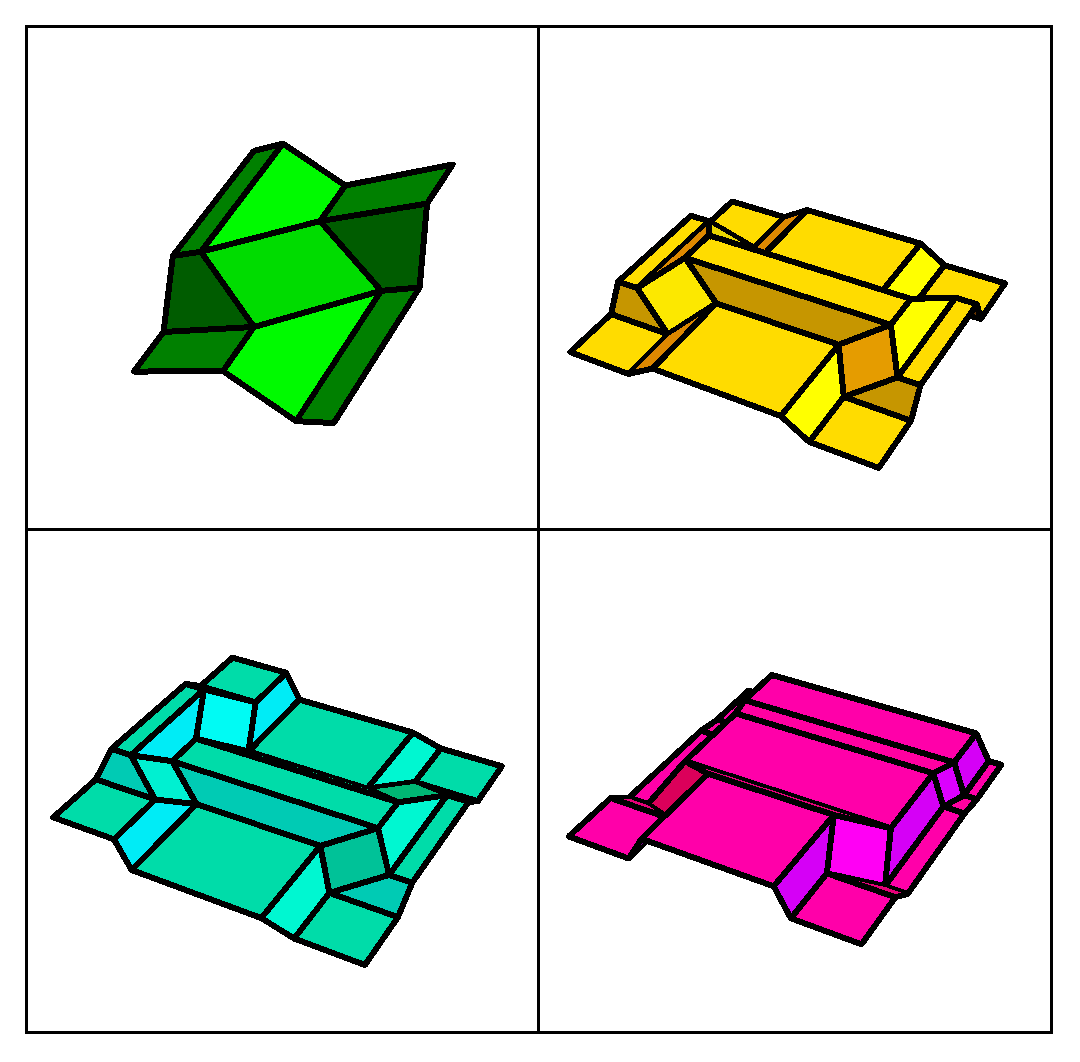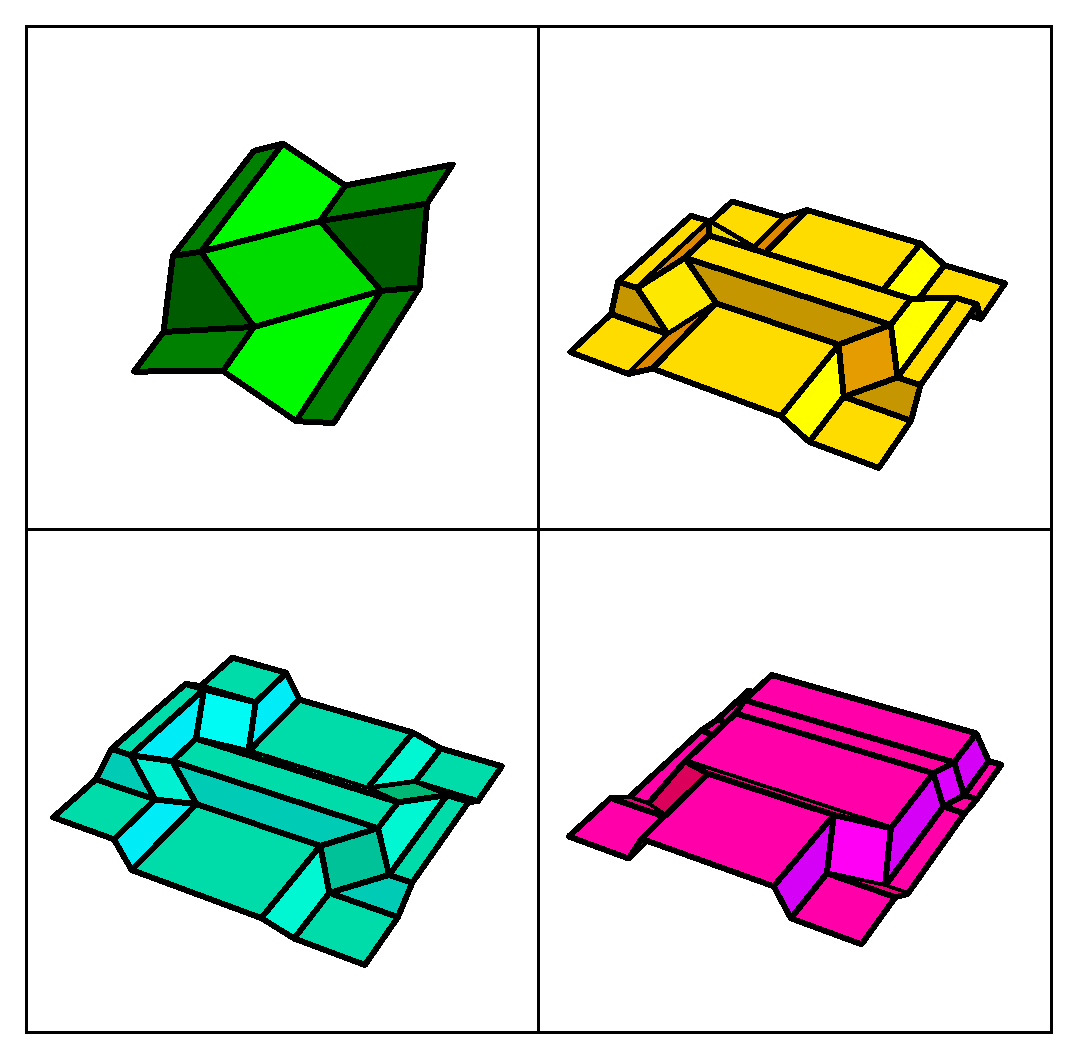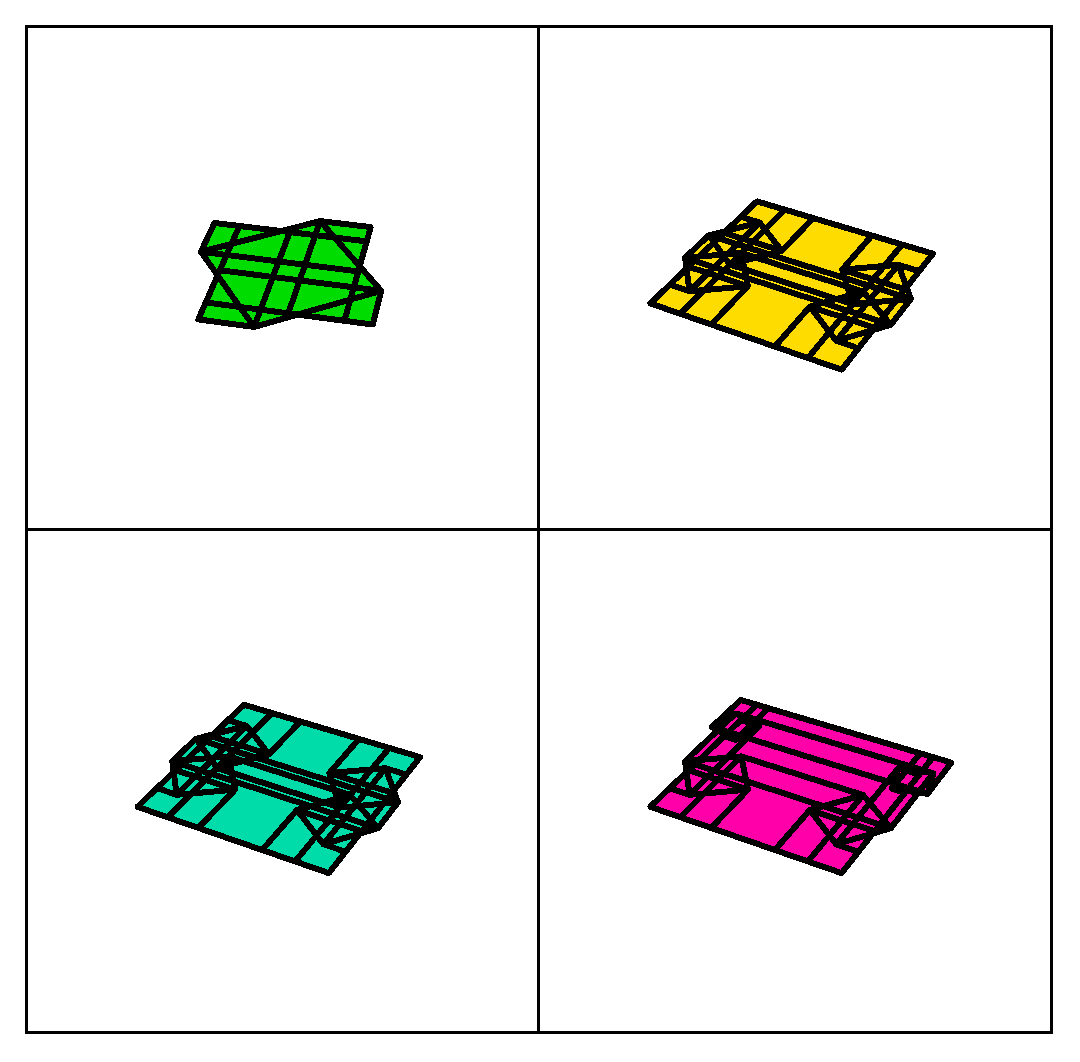
Explicit kinematic equations for degree-4 rigid origami vertices, Euclidean and non-Euclidean, Riccardo Foschi, Thomas C. Hull, and Jason S. Ku, Physical Review E, Vol. 106 (2022) 055001 (11 pages).
Mathematica code that simulates the folding table seen in Figure 8 of this paper, and shown in the black-and-white animation to the left, can be found here.
-
Rigid folding equations of degree-6 origami vertices, Johnna Farnham, Thomas C. Hull, and Aubrey Rumbolt, Proceedings of the Royal Society A, Vol. 478 (2022) 20220051 (19 pages).
- Sculpting the vertex: manipulating the configuration space topography and topology of origami vertices to design mechanical robustness, Bin Liu, Jesse L. Silverberg, Arthur A. Evans, Christian D. Santangelo, Robert J. Lang, Thomas C. Hull, and Itai Cohen, Nature Physics, Vol. 14 (2018), 811-815.
- Rigid foldability of the augmented square twist, Thomas C. Hull and Michael T. Urbanski, Origami7: Proceedings of the 7th International Meeting of Origami in Science, Mathematics, and Education, Tarquin (2018), 533-543.
- Rigid origami vertices: conditions and forcing sets, Zachary Abel, Jason Cantarella, Erik D. Demaine, David Eppstein, Thomas C. Hull., Jason S. Ku, Robert J. Lang, and Tomohiro Tachi, Journal of Computational Geometry, Vol. 7, No. 1 (2016), 171-184.
Counting valid mountain-valley assignments
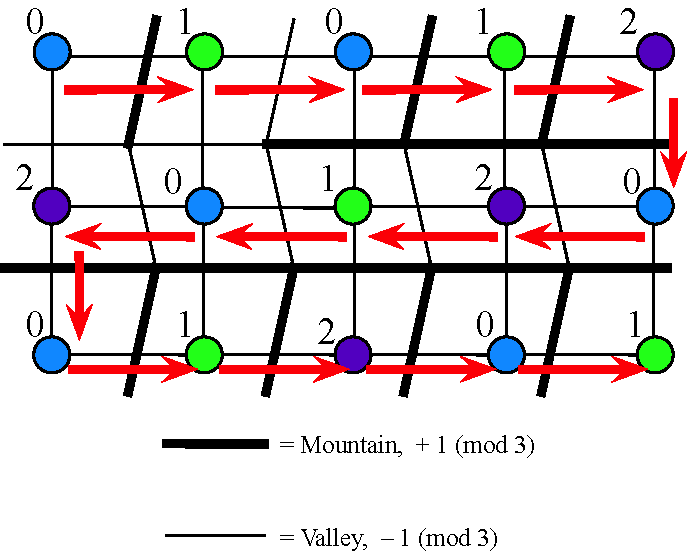
A fundamental open problem in origami is: Given an origami crease pattern, in how many different ways can we fold it? There are many ways to answer this question, but one way I'm particularly interested in is counting the number of mountain-valley (MV) assignments that make the crease pattern fold flat (can be pressed in a book without crumpling). Each MV assignment represents a distinct way in which the crease pattern can fold. The combinatorial structure of MV assignments seems very rich, even for single-vertex crease patterns. In many cases MV assignments are related to vertex-colorings of graphs, but the jury is still out on classifying the general case.
Publications:
- The origami flip graph of the 2 x n Miura-ori, Lumi Christensen, Thomas C. Hull, Emma O'Neil, Valentina Pappano, Natalya Ter-Saakov, and Kacey Yang (preprint, 2025).
- The stamp folding problem from a mountain-valley perspective: enumerations and bounds, Thomas C. Hull, Adham Ibrahim, Jacob Paltrowitz, Natalya Ter-Saakov, and Grace Wang, Discrete Mathematics and Theoretical Computer Science, Vol. 27, No. 3, 15 pages (2025).
-
Maximal origami flip graphs of flat-foldable vertices: properties and algorithms, Thomas C. Hull, Manuel Morales, Sarah Nash, and Natalya Ter-Saakov, Journal of Graphs, Algorithms, and Applications, Vol. 26, No. 4 (2021), 503-517.
- Counting locally flat-foldable origami configurations via 3-coloring graphs, Alvin Chiu, William Hoganson, Thomas C. Hull, and Sylvia Wu, Graphs and Combinatorics, Vol. 37, No. 1 (2021), 241-261.
- Face flips in origami tessellations, Hugo Akitaya, Vida Dujmović, David Eppstein, Thomas C. Hull, Kshitij Jain, and Anna Lubiw, Journal of Computational Geometry, Vol. 11, No. 1 (2020), 397-417.
- Counting Miura-ori foldings, Jessica Ginepro and Thomas C. Hull, Journal of Integer Sequences, Vol. 17 (2014), Article 14.10.8.
- Counting Mountain-Valley Assignments for Flat Folds, Thomas C. Hull, Ars Combinatoria, Vol. 67 (2003), 175-188.
Random origami
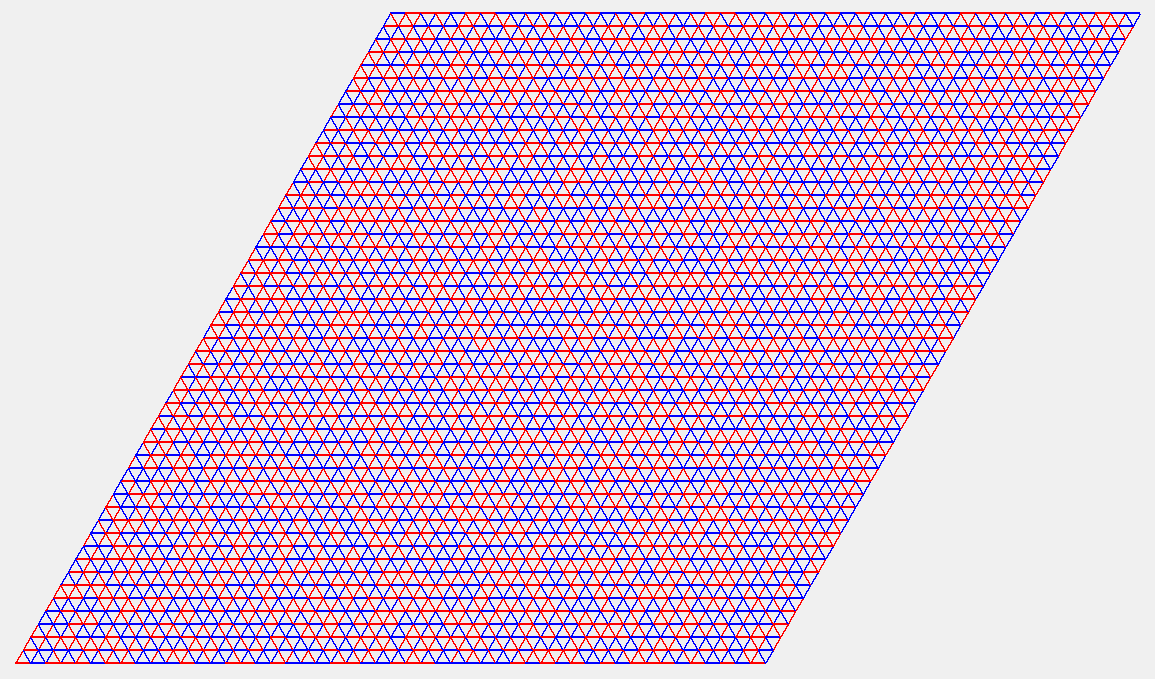
A new project that I started with Marcus Michelen and Corrine Yap is to develop a model of random, or probabalistic origami. For example, if you gave me a flat-foldable origami crease pattern and asked me to assign mountains and valleys to the creases at random (and still have it be flat-foldable), how would you do that? You can't just flip a coin for each crease, because you might end up with all mountains at a vertex, and that doesn't fold flat! So far we have one paper on our approach to this question for certain origami tessellations, where we adopt a Markov chain mixing approach to randomize a mountain-valley assignment.
Publication:
Computational geometry of folding
It seems like all aspects of origami, or folding processes in general, have interesting computational aspects to them. With numerous coauthors, and across all of my funding opportunities, we have proven many things to demonstrate that, yes indeed, origami computation is interesting! This spans solidifying how flat origami is NP-complete, to proving it is also Turing complete, to proving that rigid origami is also NP-complete. In addition, new avenues of investigation in the combinatorial geometry keep emerging, like quasigeodesics as a way to investigate unfolding polyhedral nets.
Publications:
- Flat origami is Turing complete, Thomas C. Hull and Inna Zakharevich (preprint, 2024).
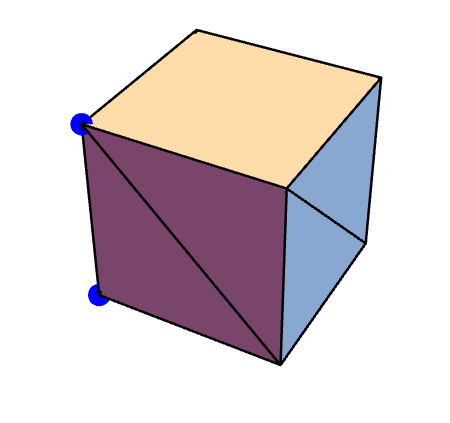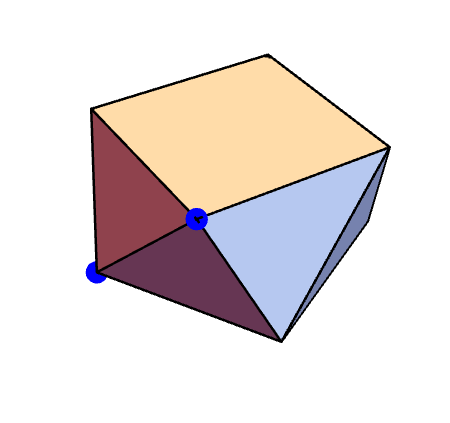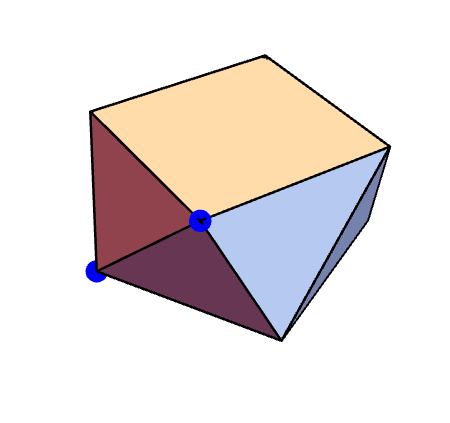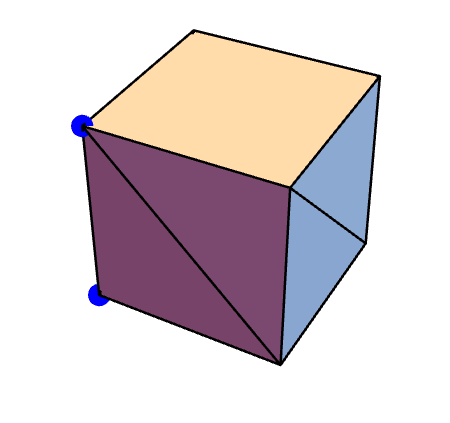
- Quasigeodesics on the cube, Hugo A. Akitaya, Erik D. Demaine, Adam Hesterberg, Thomas C. Hull, Anna Lubiw, Jason Lynch, Klara Mundilova, Chie Nara, Joseph O'Rourke, Frederick Stock, Josef Tkadlec, Ryuhei Uehara, Proceedings of the 37th Canadian Conference on Computational Geometry (preprint, 2025).
- Quasi-twisting convex polyhedra, Thomas C. Hull, Anna Lubiw, Klara Mundilova, Chie Nara, Joseph O'Rourke, Josef Tkadlec, Ryuhei Uehara, Proceedings of the 34th Canadian Conference on Computational Geometry (2022), 270-276.
- Rigid Foldability is NP-Hard, Hugo Akitaya, Erik D. Demaine, Takashi Horiyama, Thomas C. Hull, Jason S. Ku, and Tomohiro Tachi, Journal of Computational Geometry, Vol 11, No. 1 (2020), 93-124.
- Box Pleating is Hard, Hugo Akitaya, Kenny Cheung, Erik Demaine, Takashi Horiyama, Thomas C. Hull, Jason Ku, Tomohiro Tachi, Ryuhei Uehara, in Akiyama J., Ito H., Sakai T. (eds) Discrete and Computational Geometry and Graphs. JCDCGG 2015. Lecture Notes in Computer Science, Vol. 9943, Springer (2016), 167-179.
Self-folding
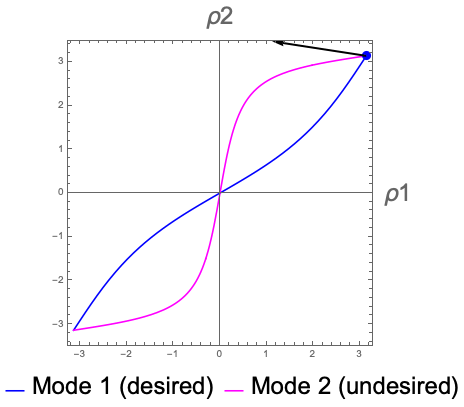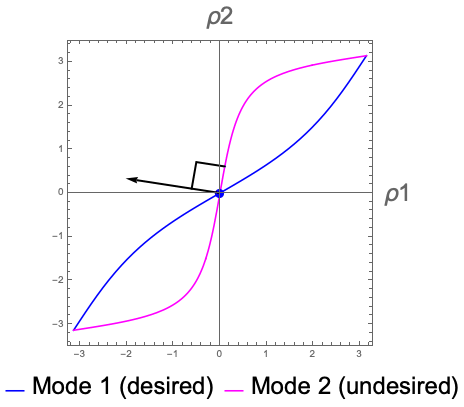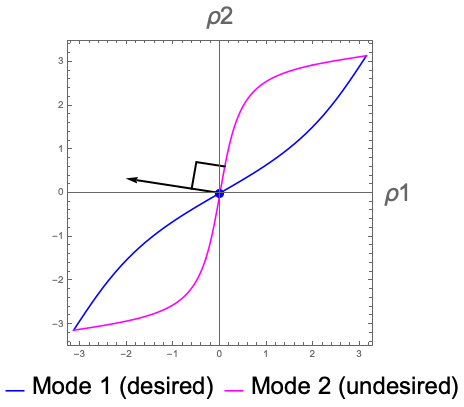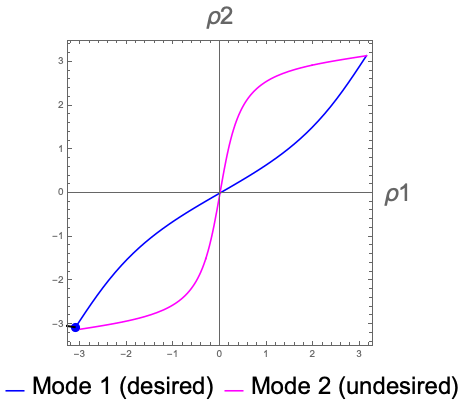
In 2015 Tomohiro Tachi and I began an investigation into modeling how and if a given rigidly-foldable crease pattern will be able to fold from the unfolded state to a target state reliably, given simple activation forces (like springs) on the creases. In other words, if we let the springs on the creases do their thing, will the crease pattern self-fold in the way we want, or will it mis-fold into some undesired shape? Our model is very theoretical (we assume mathematically thin paper, for one thing), but it had led to other studies of self-folding in the physics literature (such as in Nature Physics and Physical Review X). Our work in self-folding also won the 2016 A. T. Yang Memorial Award in Theoretical Kinematics.
Tachi and I are continuing to expand and refine our model by applying it to new developments in rigid origami configuration spaces and making it more realistic for actual materials.
Publications:
- Self-foldability of monohedral quadrilateral origami tessellations, Thomas C. Hull and Tomohiro Tachi, Origami7: Proceedings of the 7th International Meeting on Origami Science, Mathematics, and Education, Tarquin (2018), 521-532.
- Self-foldability of rigid origami, Tomohiro Tachi and Thomas C. Hull, ASME Journal of Mechanisms & Robotics, Vol. 9, No. 2 (2017), 021008-021017.
Videos:
My 2021-2022 research students, Gianna Biolo, Megan McGuinness, Taryn Padilla, and Hannah Zieminski at Western New England University created a series of TikTok videos documenting their work on fabricating self-folding origami models made of wood, plexiglass, and spring hinges. (Their attempts at using mousetrap spring hinges did not work, as they were far too strong. Fortunately, we were able to find more gentle and accurate spring hinges.) The videos are short, but they do demonstrate their work in action!
-
Video 1, showing them building their first laser-cut wood model.
-
Video 2, which is a montage of shots from their first hand-cut model with mousetrap springs, to their lasercut plexiglass and wood versions (much better). This video went semi-viral, gaining 24K views in the first 24 hours it was posted!
-
Video 3, where Megan and Hannah explain a little bit of the math that makes self-folding origami work.
-
Q&A video 1, where Gianna answers a TikTok viewer's question.
-
Q&A video 2, where Megan answers a TikTok viewer's question.
-
Q&A video 3, where Hannah and Taryn answers a TikTok viewer's question.
-
Video 4, where the students recorded me demonstrating how the larger tessellation can successfully self-fold to a desired state.