Rigid Origami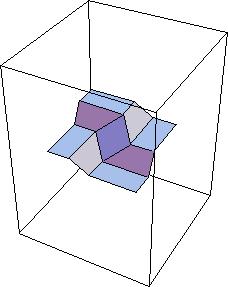
One area of origami math research that has attracted considerable interest, but for which the literature is somewhat spotty (or hard-to-find), is the subject of rigid origami. This can be summarized by the question, "Which origami models can be opened (to a completely flat, unfolded state) and closed (to the completely folded state) in a rigid manner?" By rigid, we mean that the regions of paper between crease lines do not need to bend or twist in the folding process. In other words, if we replaced the paper with sheet metal and had hinges in place of the crease lines, we could still fold the model up. People experienced with paper folding will know that there are many origami models that can not be folded rigidly. In fact, it's safer to assume that origami models are not rigid and require a proof when trying to assert that a certain fold is rigid. Who cares? Well, those seeking to use origami in industrial designs often want to know that their chosen fold is an honest-to-goodness rigid fold before devoting the resources for manufacturing, say, stiff cardboard boxes that you hope will fold up properly.
I only know of two published articles that deal with the mathematics of rigid origami. One is by the late David Huffman, of Huffman code fame. The other is by Koryo Miura, famous for his Miura map fold which is a rigid fold that has been used to deploy large solar panel arrays for space satellites. The references are:
However, the model for rigid origami that Huffman and Miura propose (which only uses some basic differential geometry) can be combined with a matrix-model for 3D folding that was first proposed by Toshikazu Kawasaki but was then made more rigorous by sarah-marie belcastro and I. The references for these papers are: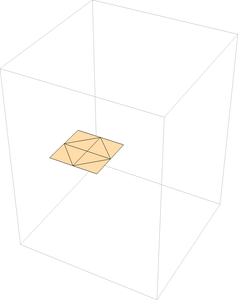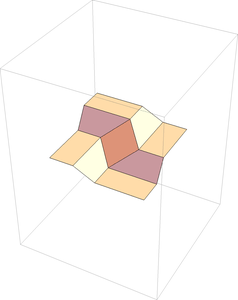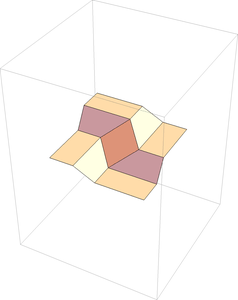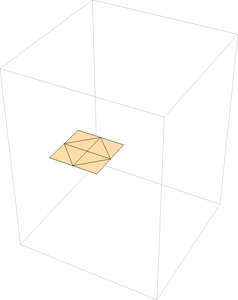 
Above is a rigid square twist fold, where we see a certain mountain-valley assignment that allows a square twist to be folded and unfolded rigidly. 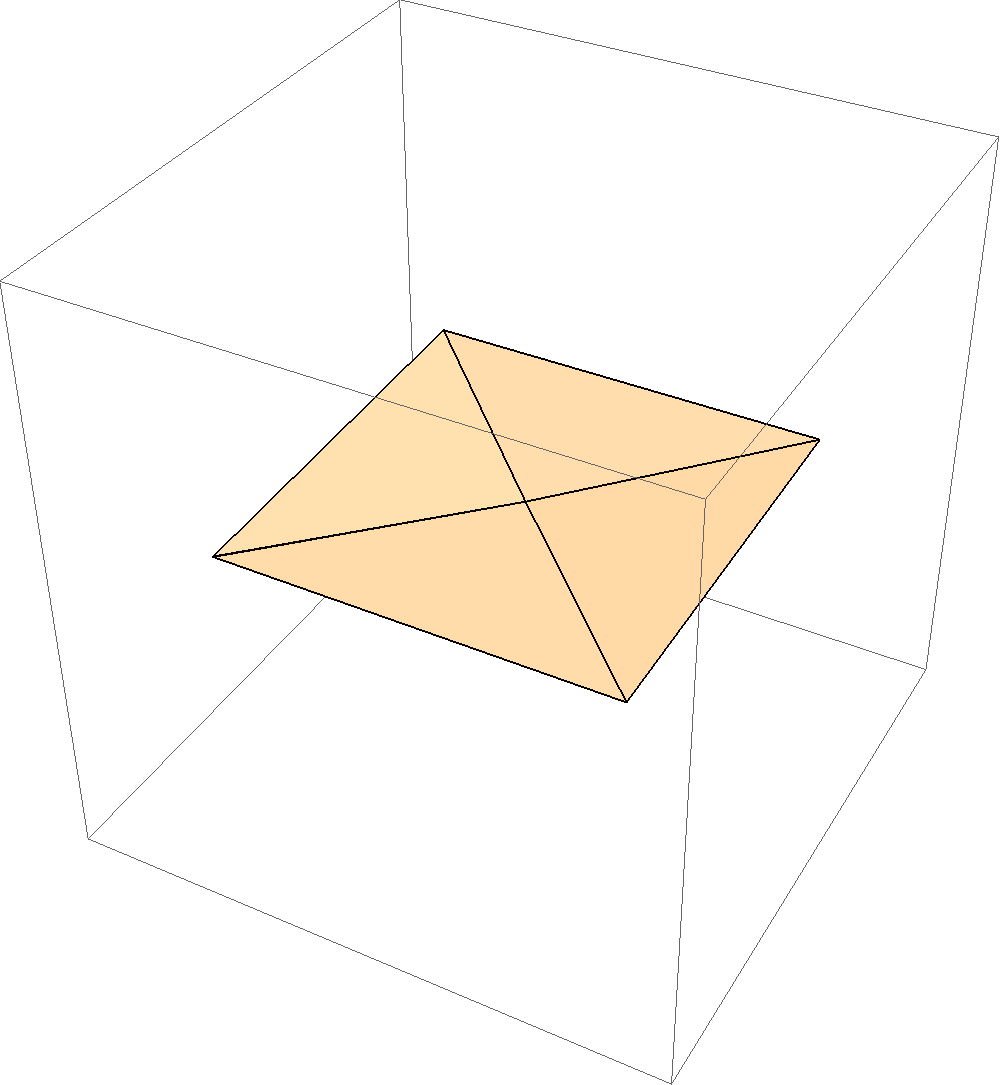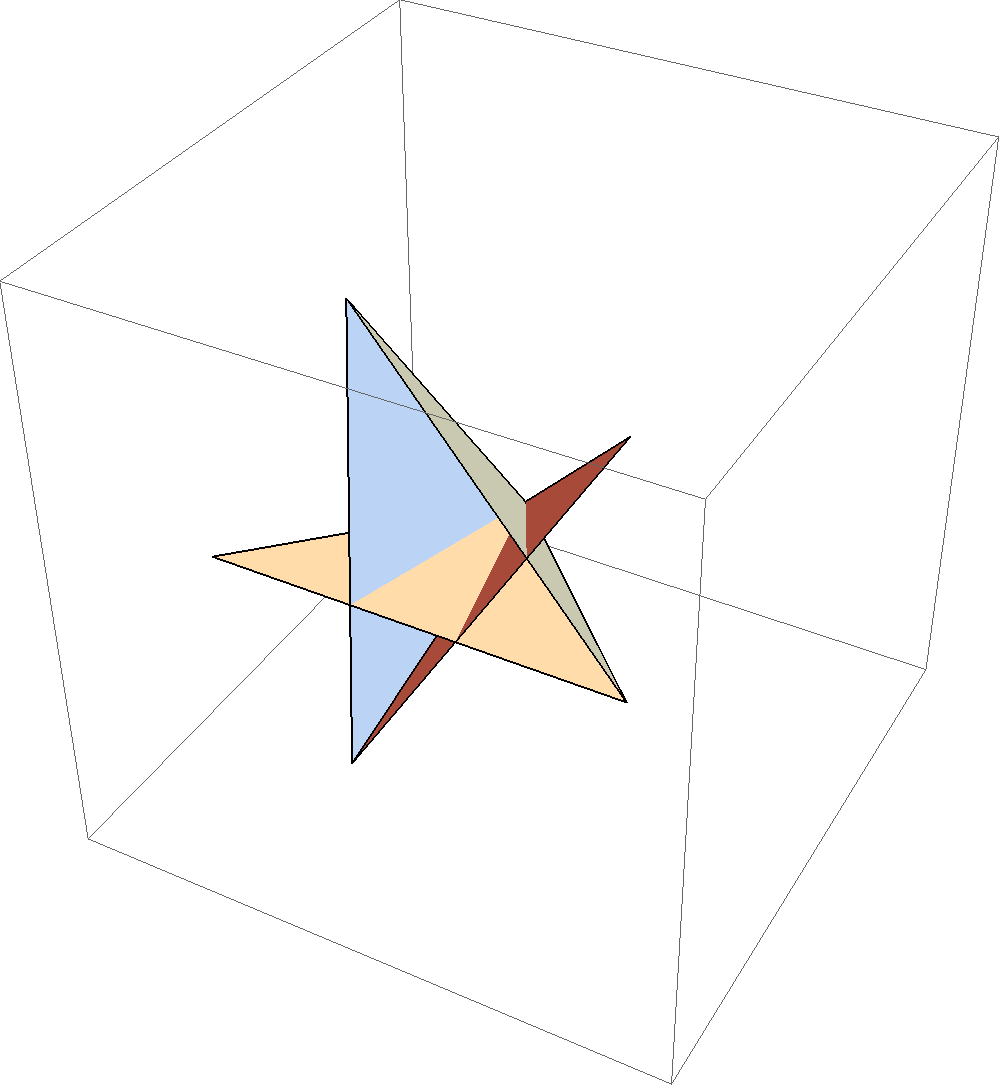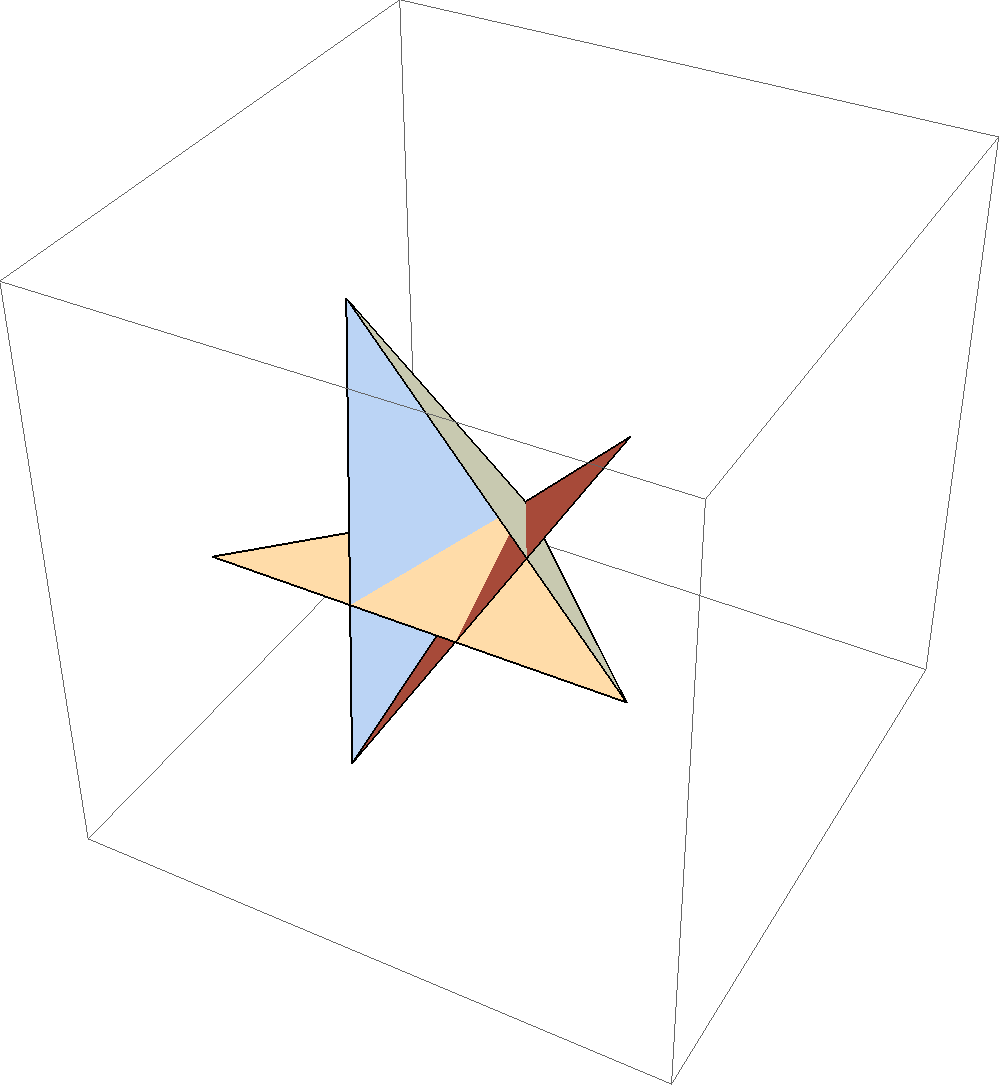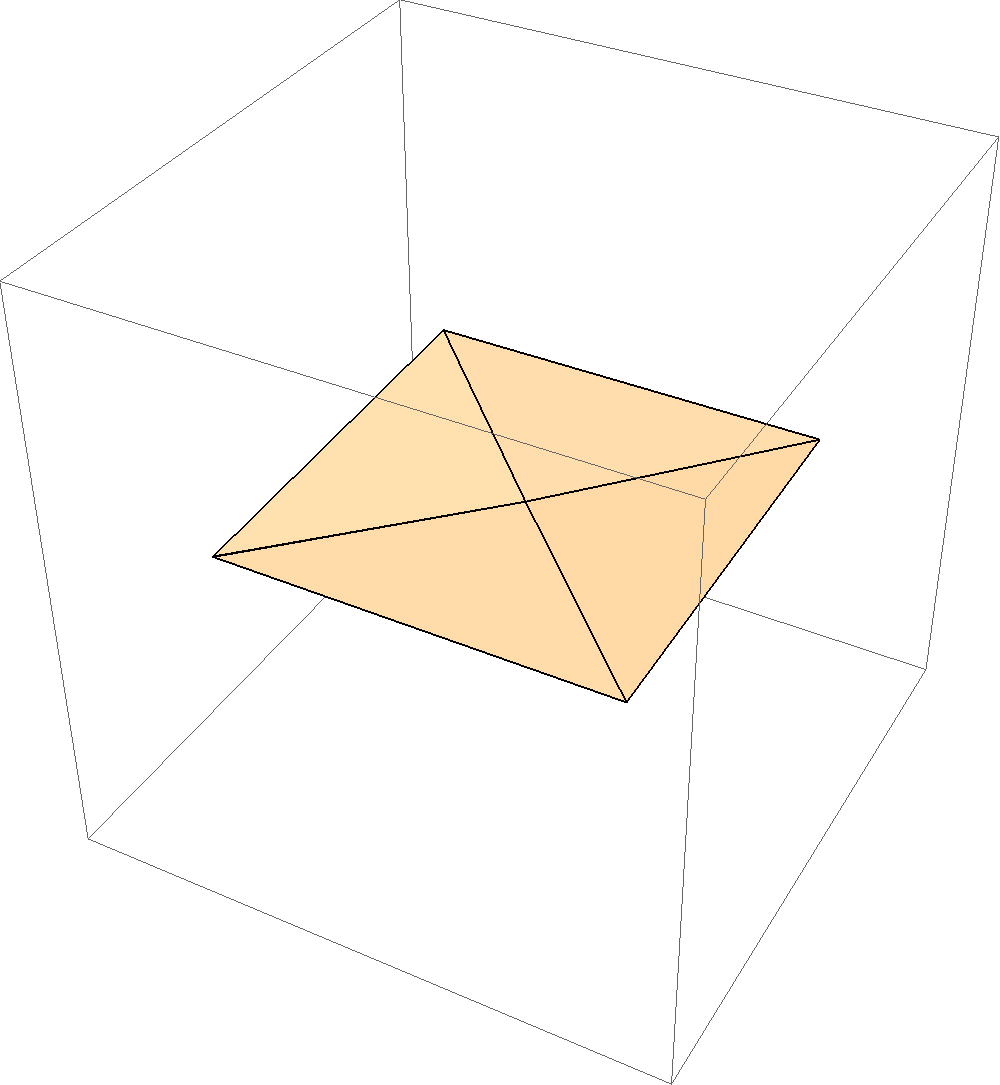 Above is shown a degree 4, all valley single vertex fold, which is impossible to do anyway, let alone rigidly. Still, it's fun to see what the matrix model does with an attempt to make all the creases be valley at a vertex. It helps illustrate how this model can serve as part of a "proof" that folds will or will not be rigid. How these animations act as "proofs":
The square twist example is strong edivence of this fold being a valid, rigid fold because we see no gaps between any of the creases as we fold and unfold it. Now, is this a proof? It's probably enough of one to convince most people, but there is another argument that can supplement this matrix model to help. This is the differential geometry approach that Miura and Huffman developed, which shows that geometrically there is nothing preventing the vertices of this model from opening and closing in a rigid manner. This, combined with the matrix model, constitutes, I think, a complete proof that the fold is rigid. One complication, however, is that the differential geometry approach only deals with single vertices. Huffman asserts that expanding this to multiple-vertex origami models follows naturally. However, in other areas of origami mathematics going from local (single-vertex) behavior to global (multiple-vertex) behavior is wrought with complications. Indeed, there are examples of origami models with more than one vertex where each vertex can fold up rigidly by themselves, but in conjunction that can't. Right now the only way to check that such complications do not arise in multiple-vertex models is on a case-by-case basis. For example, it's pretty clear that the square twist example shown above works fine. But developing a general theory on how to deal with this problem is still open. UPDATE: The above was written back in 2003, when there wasn't much research done on rigid origami. Now, that has changed. Oh, has it changed! Much work has been done by Tomohiro Tachi of the University of Tokyo on rigid origami, and there have been dozens of papers written by many people about this subject. What's more, there is a natural home for rigid origami: The study of rigidly flexible polyhedral surfaces. See, for example this paper by Ivan Izmestiev on the Classification of flexible Kokotsakis polyhedra with quadrangular base, which concerns a type of polyhedral surface with boundary and parameterizing its rigid flexibility; but if each vertex in this surface has plane angles that sum to 360 degrees, then we're talking about rigid origami. Therefore rigid origami is a special case of rigidly flexible polyhedral surfaces (with boundary). Here are some interesting papers on rigid origami (and there are lots more out there!)
These pages Copyright 2003 by Thomas Hull. Last changed 12/19/2017. |
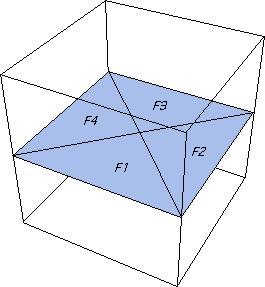Take a look at the example that doesn't work, the degree 4, all valley single vertex fold. To make this animation, I had to define four polygons in Mathematica to represent the four regions of paper in between the crease lines (shown to the right). I picked one of these regions (the bottom left one, call it F1) to remain fixed. I then used the matrix transformations to determine the position of the right-most region, call it F2, if we fold along the crease between this region and F1. Once that is done, I can figure out where the top region, F3, should be if we fold along the crease between F2 and F3. Then I can do the same thing with the left-most region, F4. In this way we start with the fixed region, F1, and proceed around the vertex, counter-clockwise, to determine the positions of all the other regions as we fold the paper up. Furthermore, I chose to do this making all of the creases valleys, with all the same folding angle.
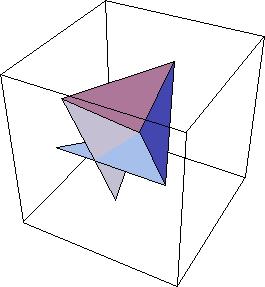The matricies used are just rotations, and thus they are isometries (they preserve distance). This means that the rigidity of the paper is preserved in our matrix transformation process. Thus, if this model, with all its valley creases, can be folded rigidly, then after we do all the transformations to the various regions of the paper (F1, F2, F3, and F4) the paper should still look continuous, with no rips. That is, region F4 and F1 should end up looking like they are attached along the crease line in between them. And sure enough, they do not! You can see this in the picture to the right, which shows the fold when the folding angle is 2 radians.